 Курсовая работа: Методы решения задач линейного программирования с n-переменными
Курсовая работа: Методы решения задач линейного программирования с n-переменными
aij - объём i-того ресурса, который расходуется на производство одной единицы j-того вида продукции i=1..m, j=1..n.
xj - объем (количество единиц) j-того вида продукции в производственном плане предприятия (j от 1 до n).
Необходимо определить нормы выпуска каждого вида продукции, чтобы прибыль от её реализации была максимальной.
Построение экономико-математической модели
Прибыль обозначим F, тогда F=c1x1+c2x2+...+cnxng max
Составим ограничения для первого ресурса:
а11 - объем первого ресурса, который расходуется на производство одной единицы первого вида продукции;
а11x1 - объём первого ресурса, который требуется на изготовление x1 единиц первого вида продукции;
а12x2 - объём первого ресурса, который требуется на изготовление x2 единиц второго вида продукции;
а1nxn - объём первого ресурса, который требуется на изготовление xn единиц n-ого вида продукции;
а11x1+a12x2+...+a1nxn - объём первого ресурса, который требуется на изготовление продукции, следовательно, мы имеем следующее ограничение:
а11x1+а12+...+а1nxn<=b1
Аналогично для остальных ресурсов:
а21x1+а22+...+а2nxn<=b2
а31x1+а32+...+а3nxn<=b3
...
аm1x1+аm2+...+amnxn<=bm
Кроме того, количество выпущенной продукции не может быть отрицательной, следовательно, x1>= 0, x2>=0, ...,xn>=0.
Таким образом, получаем следующую экономико-математическую модель задачи линейного программирования:
 (2.1)
(2.1)
Задачу линейного программирования для N (любое целое число) переменных можно представить в следующем виде:

Решения, удовлетворяющие системе ограничений условий задачи и требованиям неотрицательности, называются допустимыми, а решения, удовлетворяющие одновременно и требованиям минимизации (максимализации) целевой функции, — оптимальными .
С помощью графического метода может быть решена задача линейного программирования, система ограничений которой содержит n неизвестных и m линейно независимых уравнений, если N и M связаны соотношением N – M = 2.
Действительно, пусть поставлена задача линейного программирования.
Найти максимальное значение линейной функции
Z = c1х1+c2х2+... +cNxN
при ограничениях
a11x1 + a22x2 + ... + a1NХN = b1
a21x1 + a22x2 + ... + a2NХN = b2
. . . . . . . . . . . . . . .
aМ1x1 + aМ2x2 + ... + aМNХN = bМ
xj ≥ 0 (j = 1, 2, ..., N)
где все уравнения линейно независимы и выполняется соотношение N - M = 2.
Используя метод Жордана-Гаусса, производим M исключений, в результате которых базисными неизвестными оказались, например, M первых неизвестных х1, х2, ..., хM, а свободными — два последних: хМ+1, и хN, т. е. система ограничений приняла вид:
x1 + a1,М+1xМ+1 + a1NХN = b1
x2 + a2,М+1xМ+1 + a2NХN = b2
. . . . . . . . . . . .
xМ + aМ, М+1x2 + aМNХN = bМ
xj ≥ 0 (j = 1, 2, ..., N)
С помощью уравнений преобразованной системы выражаем линейную функцию только через свободные неизвестные и, учитывая, что все базисные неизвестные — неотрицательные: хj ≥ 0 (j = 1, 2, ..., M), отбрасываем их, переходя к системе ограничений, выраженных в виде неравенств.
Симплекс-метод решения задач линейного программирования с n-переменными
Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.
Этот метод является универсальным, применимым к любой задаче линейного программирования в канонической форме. Система ограничений здесь — система линейных уравнений, в которой количество неизвестных больше количества уравнений. Если ранг системы равен r, то мы можем выбрать r неизвестных, которые выразим через остальные неизвестные. Для определенности предположим, что выбраны первые, идущие подряд, неизвестные x1, x2, ..., xr. Тогда наша система уравнений может быть записана как
 (3.1)
(3.1)
К такому виду можно привести любую совместную систему, например, методом Гаусса. Правда, не всегда можно выражать через остальные первые r неизвестных (мы это сделали для определенности записи). Однако такие r неизвестных обязательно найдутся. Эти неизвестные (переменные) называются базисными, остальные свободными.
Придавая определенные значения свободным переменным и вычисляя значения базисных (выраженных через свободные), мы будем получать различные решения нашей системы ограничений. Таким образом, можно получить любое ее решение. Нас будут интересовать особые решения, получаемые в случае, когда свободные переменные равны нулю. Такие решения называются базисными, их столько же, сколько различных базисных видов у данной системы ограничений. Базисное решение называется допустимым базисным решением или опорным решением, если в нем значения переменных неотрицательны. Если в качестве базисных взяты переменные x1, x2, ..., xr, то решение {b1, b2,..., br, 0, ..., 0} будет опорным при условии, что b1, b2,..., br ≥ 0.
Симплекс-метод основан на теореме, которая называется фундаментальной теоремой симплекс-метода. Среди оптимальных планов задачи линейного программирования в канонической форме обязательно есть опорное решение ее системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение F самое большое. Но, во-первых, все опорные решения неизвестны и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции F не меньше, чем на старом. После ряда шагов мы приходим к опорному решению, которое является оптимальным планом.
Итак, симплексный метод вносит определенный порядок как при нахождении первого (исходного) базисного решения, так и при переходе к другим базисным решениям. Его идея состоит в следующем.
Имея систему ограничений, приведенную к общему виду, то есть к системе m-линейных уравнений с n-переменными (m < n), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще.
Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то, осуществляется переход к другому, обязательно допустимому базисному решению.
Симплексный метод гарантирует, что при этом новом решении линейная форма, если и не достигнет оптимума, то приблизится к нему. С новым допустимым базисным решением поступают так же, пока не находят решение, которое является оптимальным.
Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляется переход к другим базисным решениям, которые приближают нас к области допустимых решений, пока на каком-то шаге решения либо базисное решение окажется допустимым и к нему применяют алгоритм симплексного метода, либо мы убеждаемся в противоречивости системы ограничений.
Таким образом, применение симплексного метода распадается на два этапа: нахождение допустимого базисного решения системы ограничений или установление факта ее несовместности; нахождение оптимального решения.
При этом каждый этап может включать несколько шагов, соответствующих тому или иному базисному решению. Но так как число базисных решений всегда ограниченно, то ограниченно и число шагов симплексного метода.
Приведенная схема симплексного метода явно выражает его алгоритмический характер (характер четкого предписания о выполнении последовательных операций), что позволяет успешно программировать и реализовать этот метод на ЭВМ. Задачи же с небольшим числом переменных и ограничений могут быть решены симплексным методом вручную.
Практическая часть
Постановка задачи
Торговое предприятие планирует организовать продажу 4 видов товара A, B, C, D, учитывая при этом только два вида ресурсов: рабочее время продавцов в количестве 970 часов и площадь товарного зала 290 м2. Плановые нормативы затрат ресурсов в расчете на единицу товара каждого наименования и прибыль от их продажи заданы в таблице.
| Показатели | Товары | Общее кол-во ресурсов | |||
| A | B | C | D | ||
| Расход рабочего времени на единицу товара, ч | 0,62 | 0,81 | 0,71 | 0,43 | 970 |
| Использование площади торгового зала на единицу товара, м2 | 0,13 | 0,22 | 0,45 | 0,22 | 290 |
| Прибыль от продажи единицы товара, руб | 30 | 50 | 62 | 40 | |
Требуется определить оптимальную структуру товарооборота, обеспечивающую торговому предприятию максимум прибыли.
Математическая модель
Пусть x – количество товара, продажу которого планирует организовать торговое предприятие. Тогда x1 – товар вида A, x2 – товар вида B, x3 – товар вида C и x4 – товар вида D.
0,62x1+0,81x2+0,71x3+0,43x4 – расход рабочего времени на изготовление товара. Так как этот ресурс ограничен, имеем следующее ограничение: 0,62x1+0,81x2+0,71x3+0,43x4£970.
0,13x1+0,22x2+0,45x3+0,22x4 – использование торгового зала на изготовление товара. Так как этот ресурс ограничен, имеем следующее ограничение: 0,13x1+0,22x2+0,45x3+0,22x4£290.
Кроме того, количество выпущенной продукции не может быть отрицательной, следовательно, x1³0, x2³0, x3³0, x4³0.
Задача состоит том, чтобы найти значения x1, x2, x3 и x4 при которых полученная прибыль будет наибольшей. Прибыль обозначим F, тогда
F=30x1+50x2+62x3+40x4Þmax
Таким образом, получаем следующую экономико-математическую модель задачи линейного программирования:
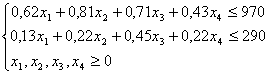
Решение задачи в MS Excel
В качестве значений переменных x1, x2, x3, x4 будем использовать ячейки $B$12:$B$15. Для значения целевой функции будем использовать ячейку $C$16.
В целевую ячейку $C$16 впишем формулу: B5*B12+C5*B13+D5*B14+E5*B15.
В ячейку $C$12 впишем формулу прибыли от товара A: B5*B12.
В ячейку $C$13 впишем формулу прибыли от товара B: C5*B13.
В ячейку $C$14 впишем формулу прибыли от товара C: D5*B14.


