Курсовая работа: Теорема Силова
Из таблицы 1 видим, что
элементами второго порядка будут: 
и, кроме того, эти элементы попарно перестоновочны. Заметим, что в A4 нет элементов шестого порядка. Действительно, a1=a1a1a1=e элемент третьего порядка,
a2=a2a2a2=e элемент третьего порядка,
a3=a3a3a3=e элемент третьего порядка,
a4=a4a4a4=e элемент третьего порядка,
a6=a6 a6 a6=e элемент третьего порядка,
a7=a7a7a7=e элемент третьего порядка,
a10=a10a10a10=e элемент третьего порядка,
a11=a11a11a11=e элемент третьего порядка.
Из приведенных вычислений следует, что в группе A4 нет элемента шестого порядка. Следовательно, искомая подгруппа A4 не изоморфна циклической группе ℤ6.
Заметим также, что в группе подстановок S3 существуют элементы второго порядка, но они не перестановочны. В самом деле, выпишем все элементы симметрической группы.
S3=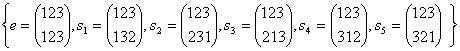
.
Построим их таблицу умножения.
Таблица 2
| e |
s1 |
s2 |
s3 |
s4 |
s5 |
|
| е | e |
s1 |
s2 |
s3 |
s4 |
s5 |
|
s10 |
s1 |
e |
s3 |
s2 |
s5 |
s4 |
|
s2 |
s2 |
s5 |
s4 |
s1 |
е |
s3 |
|
s3 |
s3 |
s4 |
s5 |
e |
s1 |
s2 |
|
s4 |
s4 |
s3 |
e |
s5 |
s2 |
s1 |
|
s5 |
s5 |
s2 |
s1 |
s4 |
s3 |
e |
Несложно видеть, что элементы s1, s3, и s5 будут элементами второго порядка, но они как видно из таблицы 2 не перестановочны, и, следовательно, никакая подгруппа группы A4 не изоморфна группе S3. Утверждение доказано.
1.3 Нормальные подгруппы. Классы сопряженных элементов
Если левостороннее
разложение группы G
по подгруппе H
совпадает с
правосторонним, то H
называют нормальной подгруппой группы G (нормальный делитель, инвариантная подгруппа)
и обозначается 
. Для любого элемента gÎG будет выполняться равенство
Hg=gH , (1)
то есть подгруппа H будет перестановочна с каждым элементом группы G.
Пусть H – нормальная подгруппа G. Определим умножение смежных классов формулой:
aH·bH=abH (2)
Ясно, что условие (1) равносильно условию g–1Hg=H.
Говорят, что элемент, а
сопряжен с элементом b посредствам элемента g, если 
. Часто используют степенные
обозначения 
.
Теорема 1.3.1. Множество всех смежных классов группы G по нормальной подгруппе H относительно умножения (2) является группой, которая называется факторгруппой группы G по H и обозначается G/H.
Доказательство. 1) Ассоциативность умножения классов вытекает из ассоциативности умножение элементов группы. Пусть g1, g2, g3 ÎG, тогда
(g1H×g2H)·g3H = (g1g2)H·g3H = g1g2g3H = g1(g2g3)H= =g1H (g2g3)H = g1H·(g2H·g3H).
2) Единицей в G/H будет смежный класс eH=H, так как HaH=eH·aH=eaH=aH. Аналогично aH·H=aH.
3) (aH)–1=a–1H, так как aH·a–1H=(aa–1)H=eH=H. ■
Покажем, что отношение сопряжения на множестве является отношениями эквивалентности. Очевидно, что всякий элемент a сопряжен с самим собой, так как a=e–1ae.
Кроме того, если элемент G сопряжен с элементом a, то есть b=g–1ag, то a=gbg–1. Следовательно, отношение сопряженности симметрично. Наконец, если b=g1–1ag1, c=g2–1bg2, то c=(g1g2)–1a(g1g2), то есть отношение сопряженности элементов транзитивно. Отсюда следует, что всякая группа G распадается на непересекающиеся множества сопряженных между собой элементов или, как говорят, на классы сопряженных элементов. ■
1.4 Нормализатор множества в группе. Центр группы
п.1. В отличие от смежных классов. Классы сопряженных элементов не все равномощны. При вычисление их мощностей решающую роль играет понятие нормализатора.
Пусть M – подмножество, H – подгруппа группы G. Нормализатором множества M в подгруппе H называется множество:
NH(M)=
,
которое, как легко проверить, является подгруппой в H. Если не указано, в какой подгруппе H берется нормализатор, то это означает, что он берется во всей группе G. Очевидно, подгруппа тогда и только тогда нормальна в группе, когда её нормализатор совпадает со всей группой.
Теорема 1.4.1. Если M – подмножество, H – подгруппа группы G, то мощность класса подмножеств, сопряженных с M элементами из H, равна индексу 
В частности,
.
Доказательство. Отобразим множества Mx, xÎH, на правые смежные классы группы H по подгруппе N=NH(M), полагая
