 Реферат: Применение новейших экономико-математических методов для решения задач
Реферат: Применение новейших экономико-математических методов для решения задач
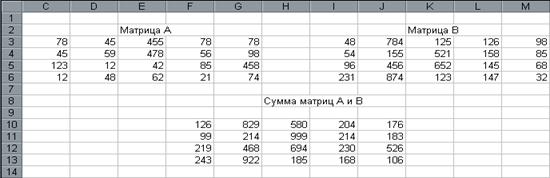
рис.8.
2.2 Транспонирование матрицы
Работу с матричной функцией ТРАНСП следует выполнять в следующем порядке:
1. Задать исходную матрицу.
2. Отметить место для матрицы-результата.
3. Обратиться к мастеру функций, найти функцию ТРАНСП и выполнить постановку задачи (рис.9.).
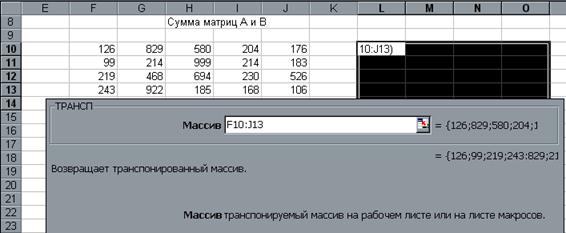
рис.9.
4. Завершить выполнение работы нажатием клавиш Shift/Ctrl/Enter (рис.10.) .
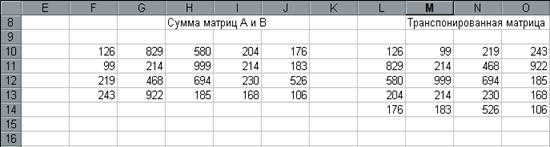
рис.10.
2.4 Вычисление обратной матрицы
Задание #4
Теперь найдем матричное выражение: Y=(FH-1)/29+K. Посчитаем определитель полученной матрицы. Поиск решения разобьем на ряд шагов:
1.Найдем матрицу обратную к матрице Н.
2.Умножим матрицы F и H-1.
3.Результат поделим на 29.
4.Сложим полученную матрицу с матрицей К.
5.Найдем определитель полученной матрицы.
Работу с матричной функцией МОПРЕД следует выполнять в следующем порядке:
1.Задать исходную матрицу.
2.Отметить место для матрицы-результата.
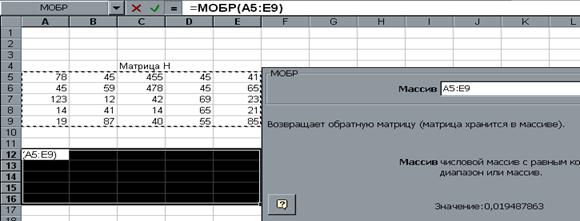 |
3.Обратиться к мастеру функций, найти функцию МОПРЕД и выполнить постановку задачи (рис.11.).
рис.11.
5. Завершить выполнение работы нажатием клавиш Shift/Ctrl/Enter (рис.12.) .
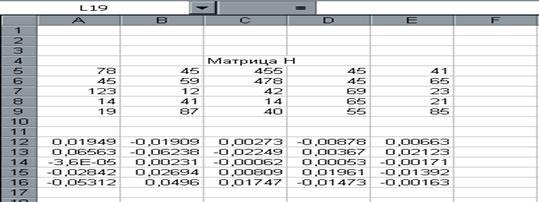
рис.12.
2.4 Умножение матриц
Надо умножить матрицы Н-1 и F. Это умножение возможно, так как число столбцов матрицы Н-1 совпадает с числом строк матрицы F.
Выполним следующую последовательность действий:
1. Зададим матрицу F.
2. Отметим место под матрицу-результат.
3. Обратимся к мастеру функций, найдем функцию МУМНОЖ и выполним постановку задачи так, как показано на рис.13. H-1
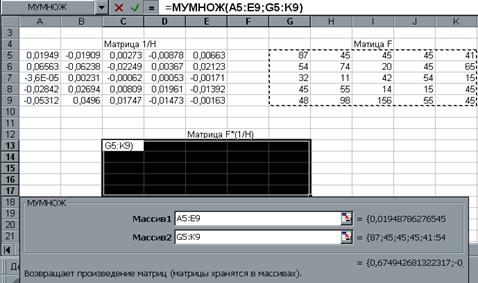
рис.13.
В качестве массива 1 указываем диапазон адресов матрицы Н-1, а в качестве массива 2 – диапазон адресов матрицы F. Для получения результата нажмем одновременно клавиши Shift/Ctrl/Enter (рис.14.).
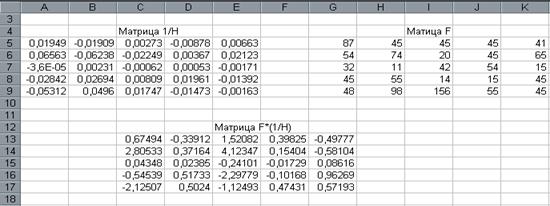
рис.14.
2.5 Умножение матрицы на число
Для умножения матрицы на число следует выполнить следующие действия:
1. Задать исходную матрицу.
2. Отметить место для матрицы-результата.
3.
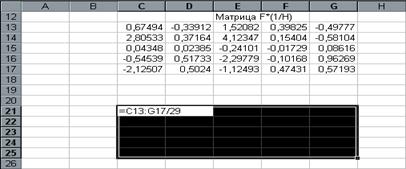 |
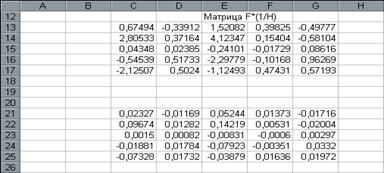
В выделенном под результат месте электронной таблицы записать произведение так, как показано на рис.15.
рис.15.
4.
 |
Завершить выполнение работы нажатием клавиш Shift/Ctrl/Enter (рис.16.).
рис.16.
2.6 Сложение матриц
Для сложения двух матриц одинаковой размерности следует выполнить следующую последовательность действий:
1.Задать две исходные матрицы.
2.Отметить место для матрицы-результата.
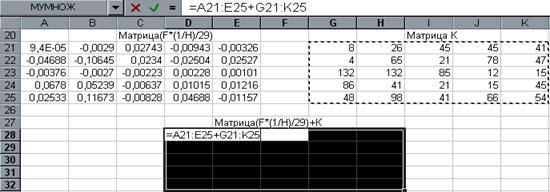 |
3.В выделенном под результат месте электронной таблицы записать сумму так, как показано на рис.17.
рис.17.
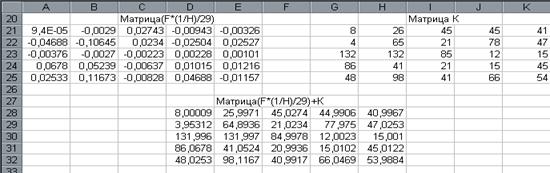 |
4.Завершить выполнение работы нажатием клавиш Shift/Ctrl/Enter (рис.18.).
рис.18.
2.7 Вычисление определителя матрицы
Для вычисления определителя матрицы сформируем лист электронной таблицы:
1.Определим исходную матрицу.
2.Определим место под результат.
3.Обратимся к мастеру функций, найдем функцию МОПРЕД , выполним постановку задачи (рис.19.).
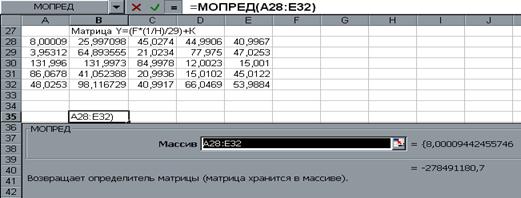
рис.19.
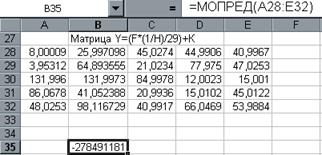 |
4.Щелкнув по кнопке ОК, получим значение определителя (рис.20.).
рис.20.
2.8 Системы линейных алгебраических уравнений
Задание #5
Решение систем линейных алгебраических уравнений всегда занимало математиков и для их решения было разработано немало численных методов, подразделяющихся на прямые и итерационные.
В EXCEL задача получения решения СЛАУ решается с помощью вышеописанных матричных функций, для чего исходную систему надо представить в виде матричного уравнения.
Рассмотрим последовательность действий для получения решения СЛАУ на конкретном примере.
![]() -12X1+12X2+23X3+6X4=120
-12X1+12X2+23X3+6X4=120
-3X1+0.3X2-3X3+X4=-25
-67X1-3X2-51X3-73X4=536 (5)
-91X1-6X2+4X3-13X4=-316
Для того, чтобы система (5) имела единственное решение необходимо и достаточно, чтобы определитель системы, составленный из коэффициентов при переменных Х1, Х2, Х3, Х4, не был равен нулю.
Рассчитаем определитель системы, пользуясь функцией МОПРЕД (рис.21.). Рассчитанное значение определителя системы равно –12. Оно не равно нулю и, следовательно, можно продолжать процесс поиска решения.
Из линейной алгебры известна матричная запись системы уравнений и матричное представление решения. Перепишем систему (5) в виде
АХ=В, где![]()
![]()
-12 12 23 6
|
-67 -3 -51 -73
-91 -6 4 -13
![]()
![]()
Х1
|
|
Х3
Х4
|
![]() -25
-25
536
-316
|
Х=А-1В, где А-1 – матрица обратная к исходной.
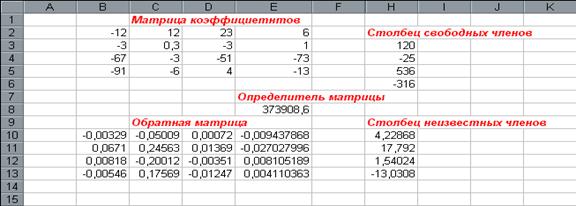
рис.21.
Результат, указанный на рис.21 можно получить, выполнив следующие действия:
1.Вычислить определитель и выяснить, имеет ли система единственное решение.
2.Вычислить матрицу обратную к исходной.
3.Найти произведение обратной матрицы и вектор столбца свободных членов.
Глава №3 Поиск решения…
3.1 Оптимизация
Почти любую ситуацию, встречающуюся в личной, деловой или общественной жизни можно охарактеризовать как ситуацию принятия решения. Для задач принятия существенными являются следующие общие элементы:
1. Множества переменных и параметров. В их число входят:
· множество разрешающих или эндогенных переменных, значения которых рассчитываются лицом, принимающим решение
· множество внешних или экзогенных переменных, значения которых не контролируются лицом, принимающим решение
· множество параметров, которые так же не контролируются и считаются в условиях задачи вполне определенными.
2. Модель – множество соотношений, связывающих все переменные и параметры.
3. Целевая функция – функция, значение которой зависит от значений эндогенных переменных. Эта функция позволяет лицу, принимающему решения оценивать варианты.
4. Численные методы – методы, с помощью которых можно систематически оценивать результаты различных решений.
Получение решения на модели, в конечном итоге, сводится к математической задаче нахождения некоторых вещественных значений эндогенных переменных, которые оптимизируют целевую функцию.
Если до недавнего времени все четыре перечисленные выше элемента ложились на лицо принимающее решение, то теперь умение пользоваться встроенными функциями EXCEL снимает наиболее утомительный пункт, а именно, применения численных методов, и делает исследование задач принятия решений более эффективными, так как теперь для решения одной и той же задачи можно быстро просмотреть различного вида постановки, в том числе и отличающиеся друг от друга по структуре.
3.2 Условный экстремум
Задание №6
EXCEL обладает мощным встроенным средством для нахождения экстремальных значений функции одной или нескольких переменных. Для одно-экстремальных функций можно найти безусловный глобальный экстремум. Для многоэкстремальных функций можно найти условный локальный экстремум.
Для функций одной переменной поиск экстремума возможен как на всей числовой оси, так и на некотором интервале. Поиск на интервале уже можно считать поиском условного экстремума функции, т.к. появляются ограничения на изменение значений аргумента.
Рассмотрим примет поиска условного экстремума функции.
Найти минимум и максимум функции Y=X5 (6)
на интервале [-1,1] и построить график.
График функции показан на рис.2.2.
Для поиска условного экстремума функции сформируем лист электронной таблицы, как показано на рис. 2.3. Функцию (6) запишем в клетку А2, где вместо переменной Х следует указать адрес ячейки А1, которая содержит начальное приближение экстремума.
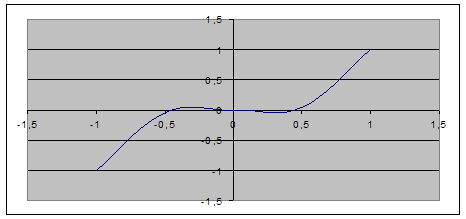
рис.22.
Для поиска минимума следует выполнить следующую последовательность действий:
1.
 |
Выполнить команду Сервис/Подбор параметра… (получим лист электронной таблицы, как показано на рис.23).
рис. 2.3
2.
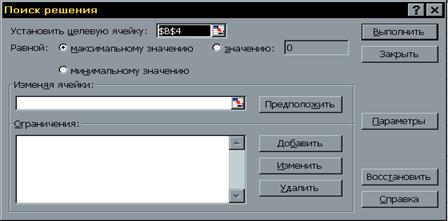 |
Заполнить диалоговое окно (рис.2.4).
рис. 2.4
2.1 Кликнуть левой клавишей мыши в поле, переместить указатель мыши и кликнуть на ячейке с формулой.
2.2 Выбрать поле Min.
2.3 В поле ввести адреса ячеек, значения которых будут варьироваться в процессе поиска решения. В нашем случае это клетка А1.
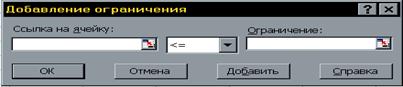
2.4 Кликнуть левой клавишей мыши в поле и затем на кнопке Добавить, откроем диалоговое окно (рис.2.2), которое заполняем, так как показано на рисунке. Так же добавляем второе ограничение.
После щелчка на кнопке ОК получим решение поставленной задачи. В клетке А1 находится значение переменной Х равное, при котором функция (6) достигает минимального значения на интервале [-1,1].
Для поиска максимума следует выполнить ту же последовательность действий, выбрав при этом поле Max. Функция (6) достигает максимального значения на интервале при значении переменной, равном (рис.26).
3.3 Математическое программирование
Анализируя возможности, можно заметить, что он применим для решения достаточно широкого класса задач математического программирования.
Если задачу принятия решений в области управления можно сформулировать в виде оптимизации вещественной функции n неотрицательных вещественных переменных подчиненных m произвольным ограничениям:
max f(x1, x2,…,xn)
при
g1 (x1,x2,…,xn)≤0
g2 (x1,x2,…,xn)≤0
…….
g3 (x1,x2,…,xn)≤0
то позволяет найти решение такой задачи, которая в формальной подстановке может быть задачей:
1.линейного программирования (когда целевая функция и все ограничения - линейны)
2.нелинейного программирования (когда, либо целевая функция, либо хотя бы одно из ограничений - нелинейны)
3.целочисленного программирования (когда ограничение целочисленности налагается на все переменные)
4.частично целочисленного программирования (когда ограничение целочисленности налагается на часть переменных)
3.3.1 Линейное программирование
Задание #7
Решить задачу линейного программирования с помощью Поиска решения…, показать графически область допустимых решений и целевую функцию. Найдем максимум функции F = -2x1 + 2x2→max при ограничениях:
x1+ x2 ≥1
-5x1 + x2 ≥0,3
x1 – x2 ≤1
x1 + x2 ≤6
x1 ≥0
x2 ≥0.
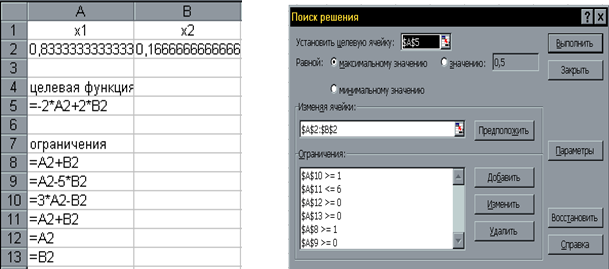 |
Сформируем страницу электронной таблицы и постановку задачи линейного программирования в диалоговом окне Поиск решения…
рис 3.3
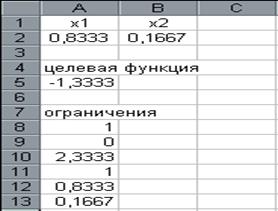 |
После выполнения поставленной задачи получаем следующие значения переменных.
рис 3.4
Как видим, при найденных значениях х1,х2 целевая функция принимает минимальное значение равное 2 и этому удовлетворяют все ограничения поставленной задачи.
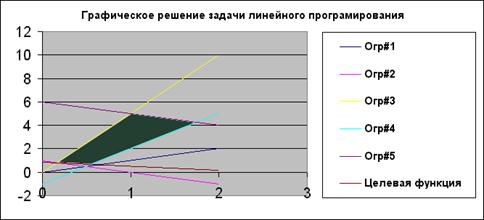 |
Графическое решение поставленной задачи выглядит так (рис. 3.5):
рис. 3.5
Задание #8
Авиакомпания МОГОЛ по заказу армии должна перевезти на некотором участке 700 человек. В распоряжении компании имеется два типа самолетов, которые можно использовать для перевозки. Самолет первого типа перевозит 30 пассажиров и имеет экипаж 3 человека, второго типа – 65 и 5 соответственно.
Эксплуатация 1 самолета первого типа обойдется 5000$ , а второго 9000$. Сколько надо использовать самолетов каждого типа, если для формирования экипажей имеется не более 60 человек.
Для начала, обозначим переменные: пусть X1 – это оптимальное количество самолетов первого типа, X2 – оптимальное количества самолетов второго типа. Очевидно, что стоимость эксплуатации самолетов должна быть минимальной. Следовательно,
5000X1 + 9000X2→min
Теперь определим ограничения. Для формирования экипажей имеется не более 60 человек, следовательно:
3X1+5X2<=60
Пассажиров надо перевезти не менее 700 человек, следовательно:
30X1+65X2>=700
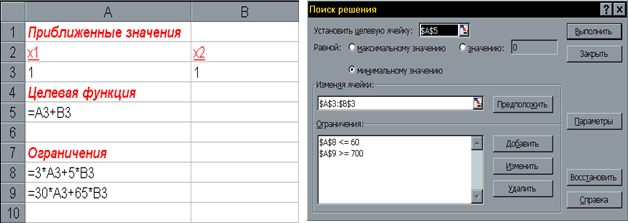
Сформируем страницу электронной таблицы и постановку задачи
линейного программирования в диалоговом окне:
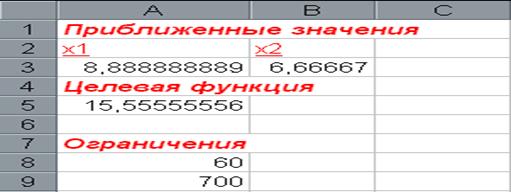 |
После выполнения поставленной задачи получаем следующие значения переменных. Как показано на рис 3.6
Рис 3.6
Т.е. нам необходимо примерно (X1=8) 8 самолётов первого класса и (X2=6) 6 самолётов второго класса, для перевозки пассажиров.
Задание #9
Решим еще одну задачу с помощью Подбор параметра…. Найдем максимум функции
F=2x1-x2+x3® max
При ограничениях:
-x1-3x2+x3≥ -5
x1+2x2+x3≤ 7
x1+x2+2x3≤ 3
x1 ≥0
x2,≥0
x3≥ 0
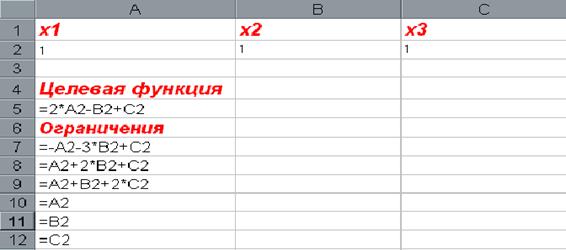 |
Сформируем страницу электронной таблицы и постановку задачи линейного программирования в диалоговом окне Подбор параметра …
Рис 4.4
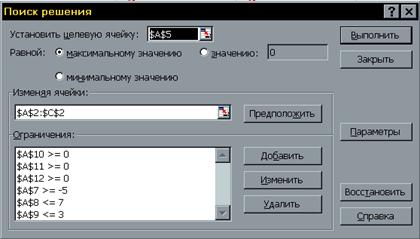
рис 4.5
После выполнения поставленной задачи получаем следующие значения переменных:
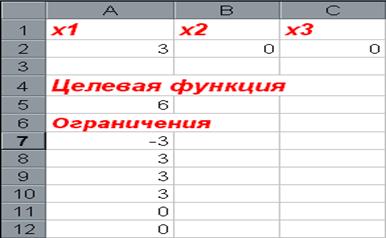
рис 4.6
Как видим, при найденных значениях целевая x1, x2, x3 функция принимает максимальное значение равное 6 и при этом удовлетворяются все ограничения поставленной задачи.
3.5 Системы нелинейных алгебраических уравнений
Задание #12
В начале рассматривался способ решения систем двух нелинейных алгебраических уравнений, имеющих специальный вид, который позволяет привести их к одному уравнению и решать это уравнение с помощью команды Подбор параметра…. Такой способ сильно сужает область систем нелинейных уравнений, подлежащих решению, так как не всегда явно можно выразить одну переменную через другую. Кроме того, с его помощью нельзя решать системы, состоящие из более чем двух уравнений.
Команда Сервис/Подбор параметра… обладает широким спектром функций, одна из которых позволяет сконструировать постановку задачи для решения систем нелинейных алгебраических уравнений. В качестве примера рассмотрим решение системы уравнений:
![]() 2А3+АВС+5А2=124
2А3+АВС+5А2=124
12В+2А=8
3С+4АС= -6
Сформируем лист электронной таблицы как показано на рис 5.5.
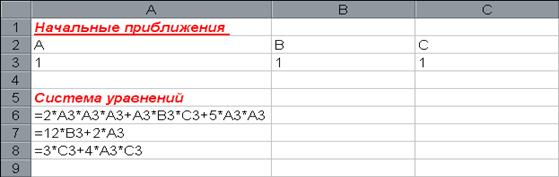
рис 5.5
Систему уравнений разместим в клетках А6, А7, А8, а вместо переменных А, В, С укажем адреса клеток А3, В3 и С3 соответственно, которые содержат приближенные значения переменных.
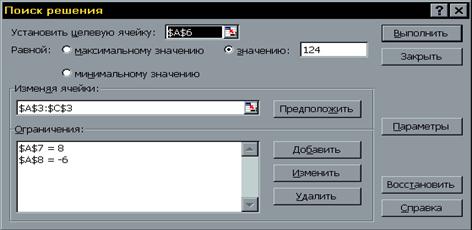 |
Для решения системы уравнений следует выполнить команду и заполнить диалоговые окна, как показано на рис 5.6.
рис 5.6
В такой постановке одно из уравнений системы (любое) выступает как целевая функция, а два других как ограничения. После щелчка на кнопке ОК в клетках А3, В3 и С3 получим решение системы уравнений (рис 5.7).
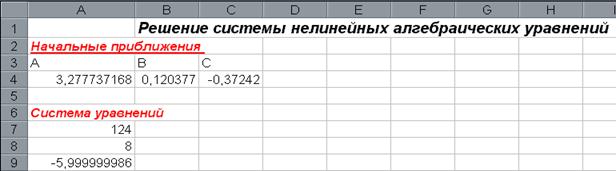
рис 5.7
Таким образом получаем, что решениями системы уравнений являются следующие значения: А=3,28 В=0,12 и С=-0,37.
Здесь, как и в ранее приведенных примерах, большое значение имеет выбор начального приближения, который может обусловить не только нахождение разных решений, но и не обеспечить нахождения ни одного. Это еще раз говорит о необходимости тщательного выбора начального приближения решения. Что можно сделать исходя из косвенных знаний об области расположения интересующего нас решения или владея методами отделения корней.
Список литературы
1. “ Microsoft Office 97“ , Эд Ботт , БИНОМ , Москва , 1998 год.
2. “ Microsoft Excel 2000 в подлиннике“ , БХВ - Санкт-Петербург ,
1999 год.


