Реферат: Расширения полей

или

p1/5(2x-1)+g(4/5+1/5(2x2+x-1))=1,

p1/5(2x-1)+g(2/5x2+1/5x+3/5)=1.

Таким образом,

y(x)= (2/5x2+1/5x+3/5).

Тогда

y(a)=y()=.

Следовательно

.

2.Составное алгебраическое расширение поля.

2.1. Конечное расширение поля.

   Пусть P — подполе поля F. Тогда мы можем рассматривать F как векторное пространство над P, т. е. рассматривать векторное пространство +F, +, {wl½l P},,

где wl- операция умножения  элементов  из F на скаляр lP.

   Определение. Расширение F поля P называется конечным, если F, как векторное пространство над P, имеет конечную размерность. Эта размерность обозначается через [F : P].

   Предложение 2.1. Если a — алгебраический элемент степени n над P, то [P (a):P]=n.

Это предложение непосредственно следует из теоремы 1.5.

   Определение. Расширение F поля P называется алгебраическим, если каждый элемент из F является алгебра­ическим над P.

   Теорема 2.2. Любое конечное расширение F поля P является алгебраическим над P.

   Доказательство. Пусть n-размерность F над P. Теорема, очевидно, верна, если n = 0. Предположим, что n>0. Любые n+1 элементов из F линейно зависимы над P. В частности, линейно зависима система элементов 1, a, ..., an, т. е. существуют в P такие элементы      с0, с1,…,cn не все равные нулю, что с0×1+ с1a+…+cn an = 0.

Следовательно, элемент a является алгебраическим над P.

   Отметим, что существуют алгебраические расширения поля, не являющиеся конечными расширениями.

2.2. Составное алгебраическое расширение поля.

 

   Расширение F поля P называется составным,  если  существует

возрастающая  цепочка  подполей  L i поля F такая, что

P = L0 — L1 —…— Lk= F   и k>1.

Теорема 2.3. Пусть F — конечное расширение поля L  и L — конечное расширение поля P. Тогда F  является конечным расширением поля P  и

(I)        [F : P] = [F : L]@[ L : P].

   Доказательство. Пусть

(1)  a1,…,am — базис поля L над P (как векторного  пространства) и

(2)  b1,…,bn — базис поля F над L . Любой элемент d  из  F можно линейно выразить через базис:

(3)  d = l1b1+...+lnbn  (lk L).

Коэффициенты 1k можно линейно выразить через базис (1):

(4)  lk = p1k a +…+ pmk am  (pikP).

Подставляя выражения для коэффициентов lk в (3), получаем

d =    å  pik aibk.

i{1,…,m}

k{1,…,n}

Таким образом, каждый элемент поля F  представим в виде линейной комбинации элементов множества B, где

B = { a ibk½{1,..., m}, k  {l,..., n}}.

Отметим, что множество B состоит из nm элементов.

   Покажем, что B есть базис F над полем P. Нам надо показать, что система элементов множества B линейно независима. Пусть

(5)  åcikaibk = 0,

       I,k

где cik  P. Так как система (2) линейно независима над L , то из (5) следуют равенства

(6)  с1ka 1+...+сmka m = 0 (k = 1,..., n).

Поскольку элементы a 1, ..., a m линейно независимы над P, то из (6) следуют равенства

c1k = 0,…,cmk = 0  (k = 1, ..., n),

показывающие, что все коэффициенты в (5) равны нулю. Таким образом, система элементов B линейно независима и является базисом F над P.

   Итак установлено, что [F , P] = nm = [F: L]×[L: P]. Следовательно, F является конечным расширением поля P и имеет место формула (I).

   Определение. Расширение F поля P называется составным алгебраическим, если существует возрастающая цепочка подполей поля P

P = L0 — L1 —…— Lk= F   и k>1 (1)

такая, что при i = 1,..., k поле L i является простым алгебраическим расширением поля     L i-1.  Число k назы­вается длиной цепочки (1).

   Следствие 2.4. Составное алгебраическое расшире­ние F  поля P является конечным расширением поля P.

Доказательство легко проводится индукцией по длине цепочки (1) на основании теоремы 2.3.

   Теорема 2.5. Пусть a1,..., ak — алгебраические над полем P элементы поля F . Тогда поле P(a1,..., ak) является конечным расширением поля P.

   Доказательство. Пусть

L 0 = P, L 1 = P [a1], L 2= P [a1, a2,],..., L k = P [a1 ,..., ak].

Тогда L1 = P [a1] есть простое алгебраическое расшире­ние поля L0; L2 есть простое алгебраическое расширение поля L1 , так как

L2 = P [a1,a2] = (P [a1])[a2] = L1[a2] = L1(a2)  и т. д.

   Таким образом,

P = L0 — L1 —…— Lk= F  

где Li = Li-1(ai ) при i = 1, ..., k, т. е. каждый член цепочки (2) является простым алгебраическим расширением предшествующего члена цепочки. Итак, поле F является составным алгебраическим расширением поля P. Следовательно, в силу следствия 2.4 поле F  является конеч­ным расширением поля P .

   Следствие 2.6. Составное алгебраическое расшире­ние поля является алгебраическим расширением этого поля.

2.3. Простота составного алгебраического расширения поля.

   Теорема 2.7. Пусть числовое поле F есть составное алгебраическое расширение поля P . Тогда F является простым алгебраическим расширением поля P.

   Доказательство. Пусть P —L — F ,  причем L = P(a), F = L(b) и, следовательно, F = P(a, b).

   Пусть f и g — минимальные полиномы над P соответственно для чисел a и b и deg f = m, deg g = n. Полиномы f и g неприводимы над P и, следовательно, не имеют в поле E комплексных чисел кратных корней. Пусть

a = a1 ,..., am — корни полинома f в C и

b = b1 ,..., bn — корни полинома g в C.

Рассмотрим конечное множество М:

M = {(ai-a)/(b-bk)½i0{1,…,m}, k0{2,…,n}}.

Поскольку P  — числовое множество (и, значит, бесконеч­ное), то в P существует число c, отличное от элементов множества М, c0P(М, cóМ. Пусть

(1)  g = a + cb.

Тогда выполняются соотношения

(2)  g ¹ ai +cbk = (i0{1,..., m}, k0{2, ..., n}).

В самом деле, в случае равенства a +сb = ai+сbk было бы

с = (ai-a)/(b-bk) 0 M

что противоречило бы выбору числа c.

   Пусть F1 = P (g) и F1 — кольцо полиномов от x. Пусть h = f(g - cx) — полином из F1[x] (g, c0P(g) = F1). Покажем, что x-b есть наибольший общий делитель полиномов h и g в кольце F1[x]. Так как g(b) = 0, то x-b делит g в E[x]. Далее, в силу (1)

h(b) = f(g-cb) = f(a) = 0.

Поэтому x-b делит полином h в E[x].  Таким образом, x-b есть общий делитель h и g в кольце E[x].

   Докажем, что g и h в С не имеет корней, отличных от b. В самом деле, допустим, что bk, k0{2 ,..., n}, есть их общий корень. Тогда h(bk) = f(g -  сbk) = 0. Сле­довательно, найдется такой индекс i0{1 ,..., m}, что g = ai+cbk (k>1), а это противоречит (2). На основании этого заключаем, что x-b есть наибольший общий дели­тель g и h в E[x]. Поскольку x - b — нормированный полином, то отсюда следует, что x - b является наиболь­шим общим делителем g и h в кольце F1[x]. Поэтому

(x-b) 0 F1[x]  и  b 0 F1 = P(g).

Кроме того, a = g - cb 0 F1.  Таким образом,

F = P(a, b)Ì F1, F1ÌF.

Следовательно, F = P(g). Далее, так как g (как и всякий элемент из F) есть алгебраический элемент над P  и F  = P (g), то поле F  = P (g) является искомым простым алгебраическим расширением поля P.

2.4. Поле алгебраических чисел.

   В классе подполей поля комплексных чисел одним из наиболее важных является поле алгебраических чисел.

   Определение. Алгебраическим числом называется комплексное число, являющееся корнем полинома поло­жительной степени с рациональными коэффициентами.

Отметим, что алгебраическое число есть любое комплексное число, алгебраическое над полем Q. В частности, любое рациональное число является алгебраическим.

   Теорема 2.8. Множество A всех алгебраических чисел замкнуто в кольце E = +С, +, —, •, 1, комплексных чисел. Алгебра A = +А, +, —, •, 1, является полем, подполем поля E.

   Доказательство. Пусть a и b — любые элементы из А. По следствию 2.6, поле Q(a, b) является алгебраическим над Q. Поэтому числа a+b, -а, ab, 1 являются алгебраическими, т. е. принадлежат множеству A. Таким образом, множество А замкнуто относительно главных операций кольца E. Поэтому алгебра A — подкольцо кольца E — является кольцом.

   Кроме того, если a —ненулевой элемент из А, то a-1 0 Q (a, b) и поэтому а-1 принадлежит А. Следовательно, алгебра A есть поле, подполе поля E.

   Определение. Поле A = +А, +, —, •, 1, назы­вается полем алгебраических чисел.

   Пример.

Показать, что число a=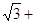 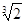является алгебраическим.

   Решение. Из a=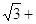 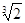следует a-.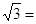

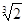Возведем обе части последнего равенства в третью степень:

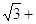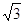a3-3a29a-3=2

или

a3 +9a-2=3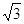(a2+1).

Теперь обе части равенства возводим во вторую степень:

a6+18a4+81a2-4a3-36a+4=27a4+54a2+27

или

a6-9a4-4a3+27a2-36a-23=0.

Таким образом a является корнем многочлена

f(x)= a6-9a4-4a3+27a2-36a-23=0

с рациональными коэффициентами. Это значит что a — алгебраическое число.

2.5. Алгебраическая замкнутость поля алгебраических чисел.

   Теорема 2.9. Поле алгебраических чисел алгебраически замкнуто.

   Доказательство. Пусть A [x] — кольцо полиномов от x над полем A алгебраических чисел. Пусть

f = а0 + а1x+... + аnхn     (а0 ,…, аn  0 A)

— любой полином положительной степени из A[x]. Нам надо доказать, что f имеет корень в А. Так как f0C[x] и поле E алгебраически замкнуто, то f имеет корень в E т. е. существует такое комплексное число с, что f(с) = 0. Пусть     L= Q(а0, ..., аn) и L (с) — простое алгебраическое расширение поля L  с помощью с. Тогда Q —L — L (c) есть конечное алгебраическое расширение поля L. По теореме 2.2, L  есть конечное расширение поля Q. В силу теоремы 2.3 L (с) является конечным расширением поля Q. Отсюда, по теореме 2.2, следует, что поле L (с) является алгебраическим расширением поля Q и, значит, c0A. Таким образом, любой полином из A[x] положительной степени имеет в A корень, т. е. поле A алгебраически замкнуто.

3. Сепарабельные и несепарабельные расширения.

   Пусть D — поле.

   Выясним, может ли неразложимый в D[x] многочлен обладать кратными корнями?

   Для того чтобы f(x) обладал кратными корнями, многочлены f(x) и fN(x) должны иметь общий отличный от константы множитель, который можно вычислить уже в D[x]. Если многочлен f(x) неразложим, то ни с каким многочленом меньшей степени f(x) не может иметь непостоянных общих множителей, следовательно, должно иметь место равенство    f '(x) = 0.

   Положим

                                            n                                                                n                

f(x) =3anxn                                    fN(x) =3nanxn-1

                                            0                                                                 1        

Так как fN(x) = О, в нуль должен обращаться каждый коэффициент:

nan = 0      (n = l, 2, ..., n).

В случае характеристики нуль отсюда следует, что an = 0 для всех n ¹ 0. Следовательно, непостоянный многочлен не может иметь кратных корней. В случае же характеристики p равенства nan = 0 возможны и для n ¹ 0, но тогда обязаны выполняться сравнения

nº0(p).

Таким образом, чтобы многочлен f(x) обладал кратными корнями, все его слагаемые должны обращаться в нуль, за исключением тех anxn, для которых nº0(p), т. е. f(x) должен иметь вид   

                            f(x) = a0+apxp+a2px2p+…

Обратно: если f(x) имеет такой вид, то fN(x)=0.

   В этом случае мы можем записать:

f(x) = j(xp).

   Тем самым доказано утверждение: В случае характеристики нуль неразложимый в D [x] многочлен f (x) имеет только простые корни, в случае оке характеристики p многочлен f(x) (если он отличен от константы) имеет кратные корни тогда и только тогда, когда его можно представить как многочлен j  от xp.

Страницы: 1, 2, 3, 4