Реферат: Методика изучения числовых систем

Перейдем теперь к изложению той методики преподавания умножения на дробь, которая получила в настоящее время признание в педагогической практике и в учебно-методической литературе. Можно подвести учащихся к новому определению умножения путем решения геометрической задачи на вычисление площади прямоугольника.

Предварительно рассматривается вычисление площади прямоугольника, у которого длины сторон - дробные числа, путем подсчета долей квадратной единицы, из которых может быть составлен прямоугольник, без знания умножения дробей.

Далее предлагаются задачи примерно такого содержания:

Вычислить площадь прямоугольника, у которого

1) основание 10 см, высота 6 см,

2) основание 7 см, высота 4 см.

Площадь первого прямоугольника учащиеся находят, пользуясь правилом для вычисления площади прямоугольника. Для второго прямоугольника преподаватель предлагает проверить справедливость правила. Учащиеся ив чертежа находят, что в одном ряду уклады­вается 7 кв. ед. и таких рядов получается 4. Следовательно, для вычисления площади, достаточно 7 умножить на 4.

Затем предлагается нарисовать прямоугольник, основание которого 4 см, а высота 1 см; затушевать на этом чертеже прямоугольник, у которого основание 4 см, а высота  см, и вычислить его пло­щадь. Учащиеся находят площадь затушеванного прямоугольника пу­тем подсчета долей квадратной единицы. После этого преподаватель указывает, что для того чтобы площадь прямоугольника вычисля­лась по одному правилу, условились и в этом случае решение за­писывать при помощи умножения длины основания на длину высоты, т.е. .

Чтобы выяснить смысл умножения 4 на , предлагается с помощью чертежа ответить на вопросы: какая площадь всего прямо­угольника? какая часть прямоугольника затушевана? какая площадь затушеванной части? Учащиеся устанавливают, что искомая площадь составляет  всей площади прямоугольника, т. е.  от 4 кв.см и равна 4 : 4 = 1 (кв. см). Следовательно, 4· - значит найти  от 4.

После этого записывают 4· = 4 : 4 = 1 (кв. см).

Затем предлагается построить второй прямоугольник, основание
 которого 4, а высота 1 см, затушевать на этом чертеже прямоугольник с основанием 4 см и высотой  см. Применить правило для вычисления площади этого прямоугольника.

Рис.12                  Рис.13

Учащиеся получают 4· . Чтобы выяснить, что это значит, устанавливают по чертежу, что искомая площадь составляет  от пло­щади всего прямоугольника и равна (4 : 4) · 3 = 3 (кв. см). Следовательно, 4· - значит найти  от 4.

Следует повторить эти рассуждения с прямоугольником, осно­вание которого 2 дм и высота 1 дм,        и установить, что значит 2·; 2·.

Вообще условились считать, что умножить число на дробь - значит найти эту дробь множимого. Умножить число на правильную дробь - значит найти часть числа, которая выражена этой дробью.

Можно показать целесообразность определения умножения на дробь на решении следующих арифметических задач.

Автомобиль едет со скоростью 45 км в час. 1) Какое расстояние он пройдет в 3 часа? в 7 часов? в  часа? в  часа?.

Записывается решение задач.

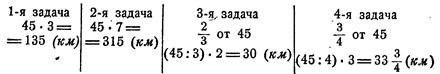
Ведутся такие рассуждения.

Условие всех задач одинаково. Дана скорость автомобиля в час и требуется узнать, какое расстояние автомобиль пройдет за неко­торое число часов. Для нахождения расстояния в 1-й и 2-й задаче скорость умножали на время. Чтобы одинаковые по смыслу задачи решались одинаковыми действиями, условились и в 3-й и в 4-й задаче называть нахождение  от 45 и  от 45 умножением 45 на  и 45 на , тогда решение 3-й задачи запишется:

Решение 4-й задачи:

Умножить 45 на  - значит найти  от 45, умножить 45 на , значит найти  от 45. После этого устанавливается то же определение умножения на дробь. Правило умножения целого числа на дробь выводится после Решения ряда примеров на основании определения. Для вывода правила следует взять такие упражнения, в которых знаменатель дроби и целое не имеют общего множителя. Например.

При умножении целого числа на смешанное число следует рас­смотреть два способа умножения, первый — множитель обращается в неправильную дробь, и умножение производится на основании установленного определения; второй — применяется распределитель­ный закон умножения Предварительно устанавливаем справедливость распределительного закона и в том случае, когда одно из слагае­мых суммы во множителе — дробь. Следует обратить внимание уча­щихся на то, что второй способ короче для тех случаев, когда ответ требуется получить в виде смешанного числа Умножение дроби на дробь прорабатывается на основании определения умно­жения на дробь

Пример. .

Ведутся такие рассуждения. Умножить  на дробь  - значит найти  от . Для этого сначала находим  от  и делим  на 3, получим . Потом, чтобы найти  от , умножаем  на 2.

Это записывается так:

Короче можно написать:

Числитель полученной дроби получился от перемножения числи­телей данных дробей, а знаменатель — от перемножения их знамена­телей После рассмотрения ряда примеров выводится правило: чтобы умножить дробь на дробь, достаточно числитель первой дроби ум­ножить на числитель второй и знаменатель на знаменатель и пер­вое произведение сделать числителем, а второе знаменателем про­изведения.

Необходимо показать учащимся на частных примерах справед­ливость основных законов умножения для дробных чисел. Приведем несколько упражнений, убеждающих в справедливости сочетатель­ного закона для дробных чисел.

Вычислить устно:

Разбираются два способа вычисления:

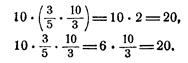
Результат получился одинаковый, следовательно,

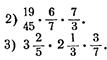
При рассмотрении умножения смешанных чисел обычный прием путем обращения смешанных чисел в неправильные дроби не вызы­вает затруднения. Следует обратить внимание на другой способ умножения смешанных чисел — умножение по частям, отдельно на целое число и на дробь. Этот способ удобен в некоторых случаях при устном счете.

Например, при умножении 6·2 выгоднее считать так:

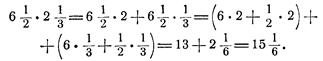
Необходимо обратить на этот способ внимание еще и потому, что учащиеся часто при устном счете неправильно им пользуются, умножая целое на целое число и дробь на дробь, и сумму полу­ченных произведений считая за искомое произведение. Неправиль­ность таких вычислений следует показать на решении конкретной задачи, лучше всего с геометрическим содержанием. Рассмотреть следующую задачу.

Построить прямоугольник, основание и высота которого 2ед. и 3ед., и найти его площадь двумя способами:

1) вычисляя сразу всю площадь, 2) вычисляя по частям.

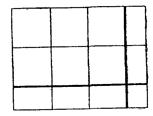
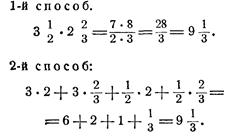                                                                                                      Рис.14                           

Учащиеся получают наглядное представление о втором способе умножения.

Полезно показать, что при вычислении вторым способом приме­няется распределительный закон умножения.

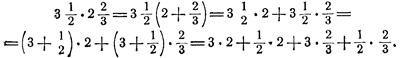
Следует подчеркнуть учащимся, что совпадение произведений, полученных 1-м и 2-м способами, показывает на справедливость распределительного закона и в том случае, когда оба сомножи­теля — смешанные числа.

Изучая умножение дробей, следует обратить внимание учащихся еще на одну особенность умножения на дробь, отличающую его от умножения на целое число.

При умножении на правильную дробь полученное произведение меньше множимого (или от умножения на правильную дробь данное число уменьшается). Следует требовать обоснование этого вывода рассуждением и иллюстрировать примерами.

Рассмотрим систему примеров на умножение на неправильную дробь.

Вывод. При умножении на неправильную дробь, не равную еди­нице, произведение получается больше множимого.

После этого следует предложить учащимся сделать общий вы­вод относительно того, в каком случае произведение получается больше множимого, в каком случае меньше множимого, в каком случае оно равно множимому. Следует задавать учащимся следую­щие контрольные вопросы. Например: на какое число нужно умно­жить число 5, чтобы произведение получилось больше 5? равно 5? меньше 5? Приведите примеры.

Деление на дробь

Делению на дробь предпосылается и в программе и в стабиль­ном учебнике нахождение числа по данной величине его дроби. Рас­суждения ведутся по такой схеме.

Пример. Найти число  которого равны 20.

Обозначим неизвестное число буквой х, тогда условие задачи запишется:

 от х равны 20.

Так как часть числа находится умножением, то вместо  от х можно написать х· или, пользуясь переместительным законом, · х. Следовательно, можно написать:  от х равны 20, или х· = 20, или ·х = 20, так как в случае бук­венного сомножителя принято знак умножения пропускать. Решение. 1) = 20 : 5 = 4; 2) х = 4 · 6 = 24.

Как и при нахождении дроби числа, при нахождении числа по данной величине его дроби необходимо рассмотреть различные случаи.

Определение деления числа на дробь остается то же, что и при делении целых чисел. Эту мысль необходимо подчеркнуть учащимся. Для того чтобы соблюдалась одна и та же система изучения обрат­ных действий, следует начать с повторения образования действия деления для целых чисел, затем перейти к рассмотрению примера на умножение на дробь и образовать две обратные задачи.

Например: 27 · = 12.

Составим обратную задачу, взяв за искомое число множитель. Эта задача решается делением целого числа на целое, которое рас­смотрено раньше.

Составим вторую обратную задачу, взяв за искомое множимое.

Запишем:

х·=12.

Эта задача и для дробных чисел решается действием деления 12 :  = х.

Так как х·= 12 или ·х = 12, то, чтобы найти х, мы находим число  которого равны 12, отсюда х = (12 : 4) · 9 = 27.

При помощи такого рода рассуждений, основой которых служит определение, учащиеся приходят к выводу, что при делении на дробь отыскивается число по данной величине его дроби. Рассмотрев примеры на умножение целого числа на дробь в случае дробного произведения и дроби на дробь и составив обратные задачи, уча­щиеся получают все случаи деления дробей. Проделав несколько упражнений, учащиеся выводят .правило деления целого на дробь, также дроби на дробь.

Неправильно строить изучение деления на дробь, взяв за опре­деление, что разделить какое-нибудь число на дробь - значит найти число по данной величине его дроби. Это противоречит научному построению изучения действий над числами, при котором вычитание я деление любых чисел определяются как действия, обратные сложению и умножению.

Полезно напомнить учащимся, что так как умножение обладает переместительным законом, то для отвлеченных чисел деление на дробь имеет одинаковый смысл независимо от того, какой из двух Сомножителей - множимое или множитель - является данным и какой искомым.

Но при решении конкретных задач деление на дробь в том случае, когда искомым является множитель (деление по содержанию), имеет другой смысл по сравнению с тем случаем, когда искомым является множимое. Например, рассмотрим задачу.

Из 6м проволоки нужно сделать прутики для счетов, длиною каждый по м. Сколько выйдет таких прутиков?

Для решения этой задачи 6м : м, в этом случае частное показывает, сколько раз м содержится в 6 м. или во сколько раз 6м больше м.

Для отыскания частного можно провести следующие рассуждения: 6м = м, м содержится в м 8 раз.

Но можно рассуждать и так: 6м: м = х; м · х = 6 м. Но, по переместительному закону умножения, · х = х·.

Следовательно, и в этом случае мы можем деление выполнять по тому же правилу, что и при нахождении всего числа по данной его части.

Рассмотрим вторую задачу.

Площадь одного участка га, другого га. Какую часть пло­щадь второго участка составляет от площади первого?

В этой задаче требуется найти дробь, при умножении на которую га получим га, для этого га : га. Обозначим частное через х, получим га·х=га. Но, по переместительному закону умножения, получаем: х·=. Следовательно, и в этом случае мы можем применить выведенное правило деления на дробь.

Приходим к выводу: при делении на дробь решаются двоякого рода задачи: 1) когда по дроби какого-нибудь числа ищется это число и 2) когда узнаем, сколько раз одно число содержится в дру­гом или какую дробь одно число составляет от другого. Выведен­ное правило деления на дробь годится и для случая деления по содержанию. Следует таким же образом показать, что и при деле­нии на целое число по содержанию можно пользоваться ранее выве­денным правилом. Необходимо обратить внимание учащихся, что при делении на правильную дробь в частном получается число, большее делимого. Так же как при умножении, следует рассмотреть на частных примерах возможные случаи соотношения между част­ным и делимым и установить, при каком делителе частное больше делимого, при каком — частное равно делимому, при каком — частное меньше делимого.

Не следует забывать важного значения упражнений в придумы­вании учащимися различных простых задач, которые решались бы умножением на дробь, делением на дробь. Это является крите­рием того, образовалось ли в сознании учащихся новое понятие о действии.

После того как учащиеся основательно поняли и усвоили смысл деления на дробь, можно дать понятие о числе, обратном данному, и познакомить учащихся с общим правилом деления, пригодным для всех случаев. Это правило заменяет деление на дробь умножением на число, обратное делителю, и дает возможность распространять некоторые свойства произведения на частное; оно является новым обобщением, полученным благодаря введению дробных чисел.

Необходимо обратить внимание учащихся на рациональные приемы вычислений с дробями в тех случаях, когда приходится выполнять последовательно несколько умножений и делений; следует прежде обозначить действия, затем производить возможные сокра­щения и только после этого делать вычисление. Например;

Литература

1.   Макарычев Ю.Н., Миндюк Н.Г. Алгебра в 6-8 классах М.:Просвещение/ 1988.

2.   Калягин Ю.М., Аганясян В.А., Саннинский В.Я., Луканкин Г.Л. Методика преподавания математики в средней школе. Учебное пособие для студентов физико - математических факультетов педагогических институтов. - М.: Просвещение, 1975.

3.   Ляпина С.Е. Методика преподавания математики в средней школе, 1975г.

4.   Рогановский Н. М. Методика преподавания математики в средней школе. - Мн.: Народная Асвета, 1990.

5.   Черкасов Р.С., Столяр А.А. Методика преподавания математики в средней школе / 1985.