Реферат: Ряды Фурье и их приложения
Если мы продолжим определение функции ƒ(x) при - l ≤ х <0 так: ƒ(x) = -ƒ(-x), то получим нечетную функцию, которая разлагается по синусам. Таким образом, если на отрезке [0, l] задана некоторая кусочно монотонная функция ƒ(x), то её можно разложить в ряд Фурье как по косинусам, таки по синусам.
Комплексная форма ряда Фурье для функций с периодом 2π.
Пусть ƒ(x) – функция, удовлетворяющая условиям определения:
Пусть функция ƒ(x) с периодом 2π, имеющая на сегменте [-π, π] не более конечного числа точек разрыва и абсолютно интегрируема на этом сегменте (т. е. она интегрируема на любом сегменте).
Тогда пусть ряд (2) является рядом Фурье функции ƒ(x). Преобразуем общий член этого ряда с помощью формул Эйлера, выражающих косинус и синус через показательную функцию. Имеем:
,
где 
.
Полагая ещё 
получим для частичных сумм
ряда Фурье выражение
Для новых коэффициентов cn получаем формулу (учитывая формулы an и bn).
Непосредственно видно, что
эта формула верна для n = 0 и для n < 0 (последнее видно, например, из того, что 
где 
обозначает число,
сопряженное с).
По доказанному имеем в точках дифферуемциемоcти:
Итак, в точках дифференцируемости
(26)
где
Правая часть формулы (26) представляет собой комплексную форму ряда Фурье для функции с периодом 2π.
Комплексная форма ряда Фурье для функции с любым периодом. (Романовский стр.33)
Пусть ƒ(x) – функция с периодом 2l, удовлетворяющая условиям , указанным в пункте 6. Тогда подстановка x= lt/ π приводит нас к функции ƒ(lt/ π) с периодом 2π. В силу предыдущего пункта в точках дифференцируемости имеем:
Переходя как в ряде, так и формулах для коэффициентов к старому переменному х и замечая, что t = π x / l, dt=(π / l)dx, получим в точках дифференцируемости:
(27)
где
Правая часть формулы (27),
где коэффициенты определяются равенствами (28), называется комплексной формой
ряда Фурье для функции с периодом 2l.
Основные типы уравнений математической физики.
Основными уравнениями математической физики называют (для случая функций двух независимых переменных) следующие дифференциальные уравнения с частными производными второго порядка.
1. Волновое уравнение:
К исследованию этого уравнения приводит рассмотрение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводе, крутильных колебаний вала, колебаний газа и т. д. Это уравнение является простейшим уравнением гиперболического типа.
2. Уравнение теплопроводности или уравнение Фурье:
К исследованию этого уравнения приводит рассмотрение процессов распространения тепла, фильтрации жидкости и газа в пористой среде (например, фильтрации нефти и газа с подземных песчаниках), некоторые вопросы теории вероятностей и т. д. Это уравнение является простейшим уравнением параболического типа.
3. Уравнение Лапласа:
К исследованию этого уравнения приводит рассмотрение задач об электрических и магнитных полях, о стационарном тепловом состоянии, задач гидродинамики, диффузии и т. д. Это уравнение является простейшим уравнением эллиптического типа.
В уравнениях (29), (30) и (31) искомая функция u зависит от двух переменных. Рассматриваются также соответствующие уравнения и для функций с большим числом переменных. Так, волновое уравнение с тремя независимыми переменными имеет вид:
уравнение теплопроводности с тремя независимыми переменными имеет вид:
уравнение Лапласа с тремя неизвестными переменными имеет вид:
Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах.
В математической физике под струной понимают гибкую, упругую нить. Напряжения, возникающие в струне в любой момент времени, направлены по касательной к её профилю. Пусть струна длины l в начальный момент напрвлена по отрезку оси Ох от 0 до l. Предположим, что концы струны закреплены в точках х = 0 и х = l. Если струну отклонить от её первоначального положения, а потом предоставить самой себе или, не отклоняя струны, предать в начальный момент её точкам некоторую скорость, или отклонить струну и придать её точкам некоторую скорость, то точки струны будут совершать движения – говорят, что струны начнет колебаться. Задача заключается в определении закона движения каждой точки струны в зависимости от времени.
Будем рассматривать малые отклонения точек струны от начального положения. В силу этого можно предполагать, что движение точек струны происходит перпендикулярно оси Ох и в одной плоскости. При этом предположении процесс колебания струны описывается одной функцией u (x, t), которая дает величину перемещения точки струны с абсциссой х в момент времени t.
(Н.С. Пискунов стр. 245, рис. 371)
Так как мы рассматриваем малые отклонения струны в плоскости (x, u ), то будем предполагать, что длина элемента струны М1М2 равняется её проекции на ось Ох, т. е. М1М2 = х2 – х1. Также будем предполагать, что натяжение во всех точках струны одинаковое; обозначим его через Т.
Рассмотрим элемент струны ММ′. На концах этого элемента, по касательным к струне, действуют силы Т.
(Н.С. Пискунов стр. 246, рис. 372)
Пусть касательные образуют с осью Ох углы φ и φ + ∆φ. Тогда проекция на ось Ou сил, действующих на элемент ММ′, будет равна T· sin (φ + ∆φ) – sin φ . Так как угол φ мал, то можно положить tg φ ≈ sin φ, мы будем иметь:
T sin (φ + ∆φ) – T sin φ ≈ T tg (φ + ∆φ) – T tg φ =
(здесь мы применили теорему Лагранжа к выражению, стоящего в квадратных скобках).
Чтобы получить уравнение движения, нужно внешние силы, приложенные к элементу, приравнять силе инерции. Пусть ρ – линейная плотность струны. Тогда масса элемента струны будет ρ ∆х. Ускорение элемента равно ∂2u / ∂t2. Следовательно, по принципу Даламбера будем иметь:
Сокращая на ∆х и обозначая a2 = T/ ρ, получаем уравнение движения
Это и есть волновое уравнение – уравнение колебаний струны. Для полного определения движения струны одного уравнения (35) недостаточно. Искомая функция u(x, t) должна удовлетворять ещё граничным условиям, указывающих, что делается на концах струны (х = 0 и х = ℓ), и начальным условиям, описывающим состояние струны в начальный момент (t = 0). Совокупность граничных и начальных условий называется краевыми условиями.
Пусть, например, как мы предполагали, концы струны при х = 0 и х = ℓ неподвижны. Тогда при любом t должны выполняться равенства:
u (0, t) = 0, (36)
u (ℓ, t) = 0. (36,)
Эти равенства являются граничными условиями для нашей задачи.
В начальный момент t = 0 струна имеет определенную форму, которую мы ей придали. Пусть эта форма определяется функцией ƒ(x). Таким образом, должно быть
u (x, 0) = u |t = 0 = ƒ(x). (37)
Далее в начальный момент должна быть задана скорость в каждой точке струны, которая определяется функцией φ(х):
Условия (101,) и (101, ,) являются начальными условиями.
Замечание. В частности, может быть, ƒ(x) ≡ 0 или φ(x) ≡ 0. Если же ƒ(x) ≡ 0 и φ(x) ≡ 0, то струна будет находиться в покое, следовательно, u (x, t) ≡ 0.
Как указывалось выше, к уравнению (30) приводит и задача об электрических колебаниях в проводах. Покажем это. Электрический ток в проводе характеризуется величиной ί(x, t) и напряжением υ(x, t), которые зависят от координаты х точки провода и от времени t. Рассматривая элемент провода ∆х, можем написать, что падение напряжения на элементе ∆х равно
Это падение напряжения складывается из омического, равного ίR∆x, и индуктивного , равного (∂ ί /∂ t )L∆x. Итак,
где R и L - сопротивление и коэффициент самоиндукции, рассчитанный на единицу длины провода. Знак минус взят потому, что ток течет в направлении, обратном возрастанию υ. Сокращая на ∆х, получаем уравнение
Далее, разность токов, выходящих из элемента ∆х и выходящего из него время ∆t, будет
Она расходуется на зарядку элемента, равную C∆x (∂υ /∂t) ∆t, и на утечку через боковую поверхность провода вследствие несовершенства изоляции, равную Аυ∆х∆t (здесь А – коэффициент утечки). Приравнивая эти выражения и сокращая на ∆x∆t, получим уравнение:
Уравнения (103) и (104) принято называть телеграфными уравнениями.
Из системы уравнений (103) и (104) можно получить уравнение, содержащую только искомую функцию ί(x, t), и уравнение, содержащее только искомую функцию υ (x, t). Продифференцируем члены уравнения (104) по х; члены уравнения (103) продифференцируем по t и умножим их на С. Произведя вычитание, получим:
Подставляя в последнее уравнение выражение (∂υ /∂х) из уравнения (103), получим:
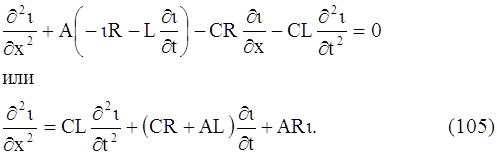
Аналогичным образом получается уравнение для определения υ(x, t):
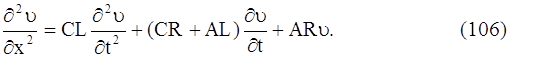
Если можно пренебречь утечкой через изоляцию (А = 0) и сопротивлением (R = 0), то уравнения (105) и (106) переходят в волновые уравнения:
где обозначено: a2 = 1/CL. Исходя из физических условий, формулируются граничные и начальные условия задачи.
Решение уравнения колебаний струны методом разделения переменных (методом Фурье).
Метод разделения переменных (или метод Фурье) является типичным для решения многих задач математической физики. Пусть требуется найти решение уравнения
удовлетворяющее краевым условиям:
u (0, t) = 0, (108)
u (ℓ, t) = 0, (109)
u (x, 0) = ƒ(x), (110)
Будем искать (не равное тождественно нулю) частное решения уравнения (107), удовлетворяющее граничным условиям (108) и (109), в виде произведения двух функций X(x) и T(t), из которых первая зависит только от х, вторая только от t:
u (x, t) = X (x) T (t). (112)
Подставляя в уравнение (107), получаем:
X (x) T′′(t) = a2 X′′(x) T(t).
Разделив члены равенства
на a2 XT
В левой части этого равенства стоит функция, которая не зависит от х, слева – функция, не зависящая от t. Равенство (113) возможно только в том случае, когда левая и правая части не зависят ни от х, ни от t, т. е. равны постоянному числу. Обозначим его через – λ, где λ > 0 ( позднее будет рассмотрен случай λ < 0). Итак,
Из этих равенств получаем два уравнения:
X′′ + λX = 0, (114)
T′′ + a2 λT = 0. (115)
Общие решения этих уравнений будут:
где A, B, C, D – произвольные постоянные.
Подставляя выражения X(x) и T(t) в равенство (112), получим:
Подберем теперь постоянные А и В так, чтобы удовлетворялись условия (108) и (109). Так как T (t) тождественно неравна нулю (в противном случае u (x, t) ≡ 0, что противоречит поставленному условию),то функция X (x) должна удовлетворять условиям (108)
и (109), т. е. должно быть Х (0) =0, Х (ℓ) = 0. Подставляя значения х=0 и х = ℓ в равенство (116), на основании (108) и (109) получаем:
0 = А · 1 + В · 0,
Из первого уравнения находим А = 0. Из второго следует:
В ≠ 0, так как в противном случае было бы Х ≡ 0 и u ≡ 0, что противоречит условию. Следовательно, должно быть
откуда
(мы не берем значение n = 0, так как в этом случае было бы Х ≡ 0 и u ≡ 0). Итак, мы получили:
Найденные значения λ называются собственными значениями для данной краевой задачи. Соответствующие им функции Х (х) называются собственными функциями.
Замечание. Если бы мы знали вместо – λ выражение + λ = k2, то уравнение (114) приняло бы вид
Х′′- k2Х = 0.
