Реферат: Ряды Фурье и их приложения

Общее решение этого уравнения:

Х = Аekx + Be -kx .

Отличное от нуля решение в такой форме не может удовлетворять граничным условиям (108) и (109).

Зная λ1/2, мы пользуясь равенством (117) , можем написать:

Для каждого значения n, следовательно, для каждого λ, выражения (119) и (120)  подставляем в равенство (112)и получаем решение уравнения (107), удовлетворяющее граничным условиям (108) и (109). Это решение обозначим un (x, t):

Для каждого значения n мы можем брать свои постоянные C и D и потому пишем Cn и Dn (постоянная В включена в Cn и Dn). Так как уравнение (107) линейное и однородное, то сумма решений также является решением, и потому функция, представленная рядом

или

также будет решением дифференциального уравнения (107), которое будет удовлетворять граничным условиям (108) и (109). Очевидно, ряд (122) будет решением уравнения (107) только в том случае, если коэффициенты Cn и Dn таковы, что этот ряд сходится в ряды получающиеся после двукратного почленного дифференцирования по х и по t.

Решение (122) должно еще удовлетворять начальным условиям (110) и (111). Этого  мы будем добиваться путем подбора постоянных Cn и Dn.  Подставляя в равенство (122)  t = 0, получим :

Если функция ƒ(x) такова, что в интервале (0, ℓ) ее можно разложить в ряд Фурье, то условие (123) будет выполняться, если положить

Далее, дифференцируем члены равенства (122) по t и подставляем t = 0. Из условия (111) получается равенство

Определяем коэффициенты Фурье этого ряда:

 

или

Итак, мы доказали, что ряд (122), где коэффициенты Cn и Dn определены по формулам (124) и (125), если он допускает двукратное почленное дифференцирование, представляет функцию u (x, t),  которая является решением уравнения (107) и удовлетворяет граничным и начальным условиям (108) – (111).

Замечание. Решая рассмотренную задачу для волнового уравнения другим методом, можно доказать, что ряд (122) представляет собой решение и в том случае, когда он не допускает почленного дифференцирования. При этом функция ƒ(x) должна быть дважды дифференцируемой, а функция φ(x) – один раз дифференцируемой.

Уравнение распространения тепла в стержне. Формулировка краевой задачи.

Рассмотрим однородный стержень длины ℓ. Будем предполагать, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. Изучим процесс распространения тепла в стержне.

Расположим ось Ох так, что один конец стержня будет совпадать с точкой х = , а другой – с точкой х = ℓ.

 

 

 

 

Пискунов стр  252, рис. 373

Пусть u (x, t) – температура в сечении стержня с абсциссой х в момент  t. Опытным путем установлено, что скорость распространения тепла, т. е. количество тепла, протекающего через сечение с абсциссой х за единицу времени, определяется формулой

где S – площадь сечения рассматриваемого стержня, k – коэффициент теплопроводности.

Рассмотрим элемент стержня, заключенный между сечениями с абсциссами х1 и х2 (х2 – х1 = ∆х). Количество тепла, прошедшего через сечение с абсциссой х1 за время ∆t, будет равно

то же самое с абсциссой х2:

Приток ∆Q1 -   ∆Q2 в элемент стержня за время ∆t будет равняться:

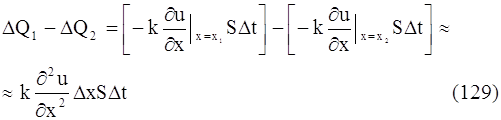
Этот приток тепла за время ∆t затратился на повышение температуры элемента стержня на величину ∆u:

или

где с – теплоемкость вещества стержня, ρ – плотность вещества стержня (ρ∆xS – масса элемента стержня).

Приравнивая выражения (129) и (130) одного и того же количества тепла ∆Q1 - ∆Q2, получим: 

Это и есть уравнение распространения тепла (уравнение теплопроводности) в однородном стержне.

Чтобы решение уравнения (131) было вполне определено, функция u (x, t)  должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Краевые условия для решения уравнения (131) могут быть различные. Условия, которые соответствуют так называемой первой краевой задаче для 0 ≤ t ≤ T, следующие:

u (x, 0) = φ(x),                                                (132)

 u (0, t) = ψ1(t),                                                (133)

 u (ℓ, t) = ψ2(t).                                                (134)

Физическое условие (132) (начальное условие) соответствует тому, что при t = 0 в разных сечениях стержня задана температура, равная φ(x). Условия (133) и (134) (граничные условия) соответствуют тому, что на концах стержня при х = 0 и при х = ℓ поддерживается температура, равная ψ1(t) и ψ2(t) соответственно.

Доказывается, что уравнение (131) имеет единственное решение в области  0 ≤ х ≤ ℓ, 0 ≤ t ≤ T , удовлетворяющее условиям (132) – (134).

Распространение тепла в пространстве.

Рассмотрим процесс распространения тепла в трехмерном пространстве. Пусть u(x, y, z, t) – температура в точке с координатами (x, y, z) с момент времени t. Опытным путем установлено, что скорость прохождения тепла через площадку ∆s, т. е. количество тепла, протекающего за единицу времени, определяется формулой (аналогично формуле  (126))

где k – коэффициент теплопроводности рассматриваемой среды, которую мы считаем однородной и изотропной, n – единичный вектор, направленный по нормали к площадке  ∆s в направлении движения тепла. Таким образом, можем записать:

где cos α, cos β, cos γ – направляющие косинусы вектора n, или

Подставляя выражение  в формулу (135), получаем:

∆Q = -k n grad u ∆s.

Количество тепла, протекающего за время ∆t через площадку ∆s, будет равно:

∆Q∆t = -k n grad u ∆t ∆s.

Вернемся к поставленной задаче. В рассматриваемой среде выделим малый объем V, ограниченный поверхностью S. Количество тепла, протекающего через поверхность S, будет равно:

где n – единичный вектор, направленный по внешней нормали к поверхности S. Очевидно, что формула (136) дает количество тепла, поступающего в объем V (или уходящего из объема V) за время ∆t. Количество тепла, поступившего в объем V, идет на повышение температуры вещества этого объема.

Рассмотрим элементарный объем ∆υ. Пусть за время ∆t его температура поднялась на ∆u. Очевидно, что количество тепла, затраченное на это повышение температуры элемента ∆υ, будет равно

где с – теплоемкость вещества, ρ – плотность. Общее количество тепла, затраченное на повышение температуры в объеме V за время ∆t, будет

Но это есть тепло, поступающее в объем V за время ∆t; оно определено формулой (136) . Таким образом, имеет место равенство

Сокращая на ∆t, получаем:

Поверхностный интеграл, стоящий в левой части этого равенства, преобразуем по формуле Остроградского (в векторной форме, где F – дивергенция векторного поля, σ – замкнутая поверхность)

полагая F = k grad u:

Заменяя двойной интеграл, стоящий в левой части равенства (137), тройным интегралом, получим:

Применив теорему о среднем к тройному интегралу, стоящего слева, получим :

где P(x, y, z) – некоторая точка объема V.

Так как мы можем выделить произвольный объем V в трехмерном пространстве, где происходит распространение тепла, и так как мы предполагаем, что подынтегральная функция в равенстве (138) непрерывна, то равенство (139) будет выполняться в каждой точке пространства. Итак,

Но

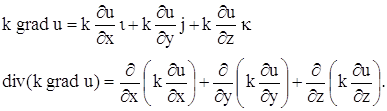
Подставляя в уравнение (140), получаем:

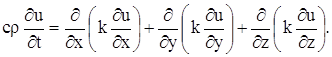
Если k – постоянное, то

и уравнение (140) в этом случае дает:

или, положив

Коротко уравнение (142) записывается так:

где ∆u – оператор Лапласа. Уравнение (142) и есть уравнение теплопроводности в пространстве. Для того чтобы найти единственное решение, отвечающее поставленной задаче, нужно задать краевые условия.

Пусть имеем тело Ω, поверхность которого σ. В этом теле рассматривается процесс распространения тепла. В начальный момент температура тела задана. Это соответствует тому, что известно значение решения при t = 0 – начальное условие:

u(x, y, z, 0) =  φ (x, y, z).                     (143)

Кроме того, должна быть известна температура в любой точке М поверхности σ тела в любой момент времени t – граничное условие:

u (М, t) =  ψ (М, t).                                   (144)

(Возможны и другие граничные условия.)

Если искомая функция u (x, y, z, t) не зависит от z, что соответствует тому, что температура не зависит от z, то получаем уравнение:

-                    уравнение распространения тепла на плоскости. Если рассматривается распространения тепла в плоской области D с границей С, то граничные условия, аналогично (143) и (144), формулируются так:

u (x, y, 0) = φ (x, y),

u(М, t) = ψ (М, t),

где φ и ψ – заданные функции, М – точка границы С.

Если же функция u не зависит ни от z, ни от y, то получаем уравнение

- уравнение распространения тепла в стержне.

2π, ƒ(x), φ, φ(x) ,[-π, π], (λ, λ +2π), ψ(x), ·, ℓ, l, < x ≤, | x |,α, β,[a, b], σ, u (x, t), М1М2 ,φ +, ∆φ ,≈, ρ, ∆, ∂, ≡, ι, ί, υ, ′, ≠, κ, k, s, u(x, y, z, t), Ωσ

Заключение

          В этой дипломной работе приведены лишь немногие примеры того как ряды Фурье позволяют решить важные задачи математической физики. Например, некоторыми из них являются задачи на распространения тепла в стержне или колебания струны. Приведены примеры нахождения периодических решений линейных дифференциальных уравнений с помощью рядов Фурье. На небольшом количестве страниц изложен материал, содержащий основные факты теории рядов Фурье.

          Работа начинается с представления функции в виде тригонометрического ряда, который и является при подставлении в него соответствующих коэффициентов (коэффициентов Фурье) рядом Фурье. Далее рассматриваются некоторые признаки сходимости рядов Фурье, вывод коэффициентов Фурье и их оценка. Представлена комплексная форма рядов Фурье. Рассмотрены примеры применений преобразований Фурье и метода Фурье (метода разделения переменных).

Так как теория тригонометрических рядов (рядов Фурье) в настоящее время достаточно велика по своему содержанию и объему, то естественно, что здесь не мог быть исчерпан весь материал.

          В заключение хотелось бы отметить, что о Фурье мы прежде всего вспоминаем как об авторе “Аналитической теории теплоты” (1822 г.). В силу общности метода эта книга стала источником всех современных методов математической физики, относящихся к интегрированию уравнений в частных производных при заданных граничных условиях.

Литература:

1.   Н.С. Пискунов „Дифференциальное и интегральное исчисления”, Москва, „Наука”, 1972 г.

2.   И.М. Уваренков, М.З. Маллер „Курс математического анализа”, Москва, „Просвещение”, 1976 г.

3.   В.С. Шипачев „Высшая математика”, Москва, „Высшая школа”, 1990г.    

4.   Г.Е. Шилов  „Математический анализ функции одного переменного”, Москва, „Наука”, 1970 г.

5.   Я.С. Бугров, С.М. Никольский „Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции      комплексного  переменного”,  Москва,  „Наука”, 1989 г.

6.   В.А. Подольский, А.М. Суходский „Сборник задач по математике для техников-программистов”, Москва, „Высшая школа”, 1978 г.

7.   Г.М. Фихтенгольц „Курс дифференциального и интегрального исчисления”, том III, Москва, „Наука”, 1969г.

8.   В.Е. Шнейдер, А.И. Слуцкий, А.С. Шумов „Краткий курс высшей математики”, том2, Москва, „Высшая школа”, 1978г.