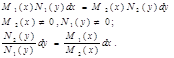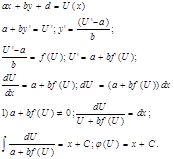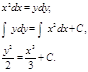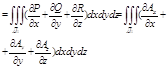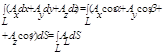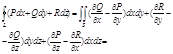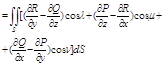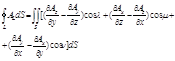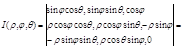Реферат: Шпора
Реферат: Шпора
Вопрос№11Если пов-ть Р задана параметрич. ур-ями
ф-ии x,y,z непрерывны с частными производными то поверхностный интеграл 1-го рода вычисл. С помощью интеграла двойного рода,взятого по обл. G по ф-ле:
Если пов-ть Р задается явным урав. Z=F(x,y)=z(x,y) Где (x,y) Часными произв.,то поверхностный интегр.1-го рода Вычисл.по ф-ле :
где P и Q соотв.часные произв. Поверхн.интеграл 2-го рода
Криволин.интеграл 2-го рода:
Пусть задана двусторонняя пов-ть S и на верхн. Стороне задана ф-ция U=F(x,y,z).Разобьем задан. Повер.S непрерывн.кривыми на конечное число Частичных поверх. S1,S2….Sn.Проэктир.эти поверх. На XOY ,
Если сущ.предел Lim s n при От способа дел.области на части и выбора точек Mi, То его наз.повер.интегалом 2-го рода по поверхн.и Обознач. :
Если же проэктировать пов-ть на другие плоскости ,то Получится:
Пусть на пов-ти заданы три ф-ции P(x,y,z), Q(x,y,z) R(x,y,z) тогда повер.интегр.2-го рода общего вида наз.
Сущ. Пл-ть такая что в каждой т.пов-ти сущ.нормаль.Обозначим Через Тогда,как и для криволин.интеграла имеет место форма между повер.Интегр.1 и 2 рода:
Пусть пов-ть S задается своими парам.ур-ми:
ф-ции x,y,z –непрерыв.и имеют непрер.частн. произв.Тогда:
Пов-ти с повер.интегралом 2-го по задан.пов-ти. Пусть задана некоторая гладкая повер.S на верхн.стороне этой повер. Заданы три ф-ии P(x,y,z),Q(x,y,z),R(x,y,z) непрерыв.и имеющ.непрер. Частн.произв.по своим аргументам и L-контур повер.,проходящий в Полож.направления.Тогда:
|
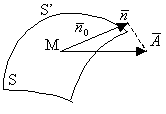
Билет №14 Поток вектора через поверхность Пусть задана некоторая
область(тело) ДÌR3 Пусть над этой областью определено поле вектора
Возьмем в области Д
некоторую поверхность S обозначим
через
Потоком вектора
Проекция вектора на ось
Ап – проекция
вектора А тогда поток вектора будет равен
|
Вопрос №16Общий вид диф уравнения F(x, y, y’)=0 y’=f(x,y) (1). Решением дифференциальное уравнение первого порядка называется всякая функция y=j(x), которая будучи подставлена в данное уравнение обращает его в тождество. j’(x)= f (x, j(x));
Задача Коши для диф. уравнения 1 порядка. Требуется найти решение диф.
ур-я (1) удовлетворяющего следующему условию Теорема Коши. Пусть задана на плоскости XOY
некоторая обл. Д и задано диф. ур-е разрешённое относительно производной,
тогда если функция f(x, y) и её частная производная принимает значение
Т.е. если существует решение диф. ур-я, то таких решений бесконечное множество. График функции являющийся решением диф. ур-я принято называть интегральной кривой, процесс решение принято называть интегрированием. Точку Решения диф. ур-я в каждой т. которого нарушается условие единственности из теоремы Коши, принято называть особым решением диф. ур-я. График особого решения называется особой кривой. Определение общего решения диф. ур-я 1 порядка: Функция y=j(x, C), где С произвольная константа, называется общим решением диф. ур-я (1) если выполнены следующие условия: 1. Функция y=j(x, C) является решением ур-я (1) при любом значении произвольной константы С; 2.
Какова бы ни была т. Частным решением данного диф. ур-я называется решение этого ур-я которое может быть получено из общего решения при некотором фиксированном значении произвольной константы С. Определение: Если решение диф. ур-я (1)
может быть получено в виде Особое решение данного диф. ур-я (1) ни при каком значении константы С не может быть получено из общего решения.. |
|||||
Вопрос №17Диф. ур-ем с разделёнными перемеными принято называть ур-е вида (1):
Если y=y(x) является решением ур-я (1), то и правая и левая части этого ур-я представляют собой дифференциалы от переменной x, т.е. имеем равенство двух дифференциалов, то тогда неопределённые интегралы отличается разве лишь на константу. Т.е. интегрируя равенство (1), получаем общее решение данного диф. ур-я:
Уравнения с разделяющимися переменными:
Уравнения, приводящиеся к уравнениям с разделёнными переменными.
Т.е.
Пример:
|
Билет №15Дивергенция , циркуляция ротор вектораПусть задана некоторая
пространственная область Д над которой определенно поле вектора Рассмотрим интеграл , выражающий поток вектора через поверхность S Обозначим Аx = P(x,y,z) , Ay =Q(x,y,z) , Az = R(x,y,z)
поверхность S ограничивает тело Д1
- расходимость
(дивергенция ) вектора
- уравнение Остроградского-Гаусса Ап – проекция
вектора Циркуляция , вихрь и ротор вектораПусть в пространстве задано некоторое тело Д и пусть в теле Д рассматривается некоторая кривая L , которая гладкая , имеет непрерывно изменяющуюся касательную Обозначим через a,b,g углы , образует касательная к кривой L с осями координат Пусть над этим телом определенно поле вектора Тогда криволинейный интеграл по кривой L
Рассуждая как и прежде можно показать , что L0 - единичный вектор касательной L1 L1 - касательный вектор к кривой L Если кривая L
является замкнутой кривой , то такой интеграл принято называть циркуляцией
вектора Пусть теперь в некоторой области Д задана поверхность S , контур которой обозначим через L
- формула Стокса
Ротором векторного поля
Циркуляцией вектора
|
Билет №13Криволинейные интегралы в пространстве и объем тела в криволинейных координатахПусть в пространстве OXYZзадано тело G.И пусть в другом пространстве OUVW задано тело Д И пусть заданы 3 функции
взаимно однозначно отображающие область Д в области G Будем считать функции x,y,z –непрерывными и имеющие непрерывные частные производные Рассмотрим Якобиан
Можно показать , что в случае взаимно однозначного отображения области Д и G якобиан ни в одной точке области Д не обращается в 0 А значит в области Д сохраняет один и тот же знак Координаты (U,V,W) принято называть криволинейными координатами точек области G И тогда можно показать , что объем области G в криволинейных координатах выражается по следующей формуле
Если теперь в области G будет задана функция f(x,y,z) –непрерывная в этой области, то справедлива следующая формула замены переменных в тройном интеграле
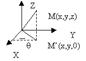
При замене переменных в тройном интеграле наиболее часто используются цилиндрические и сферические координаты Под цилиндрическими координатами следует понимать объединение полярных координат на плоскости XOY и аппликаты z r,q,z
r-расстояние от начала координат до проекции тМ на плоскость q-угол , образованный радиус вектором ОМ , в пол направлении
0£ r < +¥ , 0£ q < 2p , -¥< z < +¥ Подсчитаем якобиан в случае цилиндрических координат
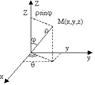
q- угол , образованный проекцией радиус-вектора тМ j-угол, образованный радиус-вектором тМ r- радиус-вектор тМ, равный ОМ Сферическими координатами принято называть r,j,q Где r- расстояние от начала координат до тМ j- угол , образованный радиус-вектора с осью Z q- угол, образованный проекции радиус-вектора с осью X r=(ОМ) 0£ r < +¥ , 0£ j < p , 0 < q < 2p Найдем якобиан для сферических координат
=cosj[r2 cos2 qcosj sinj + r2 sin2 q sinj cosj] + rsinj [r sin2 j cos2 q + r sin2 j sin2 q] =r2 cos2 j sinj + r2 sin3 j=r2 sin j I(r,j,q)=r2sinj |
|||||