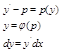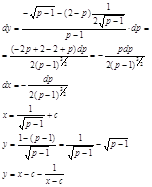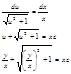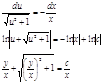Реферат: Шпора
Реферат: Шпора
Вопрос №18 Пусть
задана функция
Пример:
Определение: диф. ур-е 1 порядка разрешённое относительно производной называется однородным диф. ур-ем 1 порядка, если его правая чаcть (функция f(x,y)) является однородной функцией 0-й степени. Метод
решения: Пусть (1) является однородным уравнением
2)
если т.е.
|
Билет№20 Линейные диф. Уравнения1- порядка. Метод подстановки. Линейным уравнением 1-го порядка называют уравнения вида: (1) y’+yP(x)=Q(x) – где P(x) и Q(x) некоторые функции переменной х , а y’ и y входят в уравнение в 1 степени. 1.Метод подстановки: Будем искать решение уравнения 1 в виде произведения y=U(x)V(x) при чём так, что мы можем подобрать одну из функций по желанию, а вторую так, чтобы удовлетворяла (1) : y’=U’V+UV’ ; U’V+UV’+UV*P(x)=Q(x) ; U’V+U(V’+V*P(x))=Q(x) Найдём V ,чтобы V’+VP(x)=0 :
y’+y cos(x)=1/2 sin(2x) y=UV U’V+UV’+UVcos(x)=sin(x)cos(x) V’+Vcos(x)=0 dV/V=-cos(x)dx ln(V)= -sin(x) V=e-sin(x)
sin(x)=t
|
Билет №22Уравнение Бернулли и Рикотти и их решение. Уравнение Бернулли – это диф. Ур-е следующего вида :
где P(x) и Q(x) – непрерывные функции m – действительное число ¹0 и ¹1 разделим уравнение на ym :
Обозначим через
теперь подставим в уравнение
получили линейное уравнение . Уравнение Рикотти – это диф. следующего вида Где P(x),q(x),r(x) – некоторые непрерывные функции Рассмотрим несколько случаев 1) если ф-ции P(x) , Q(x) и r(x) – явл. Константами то в этом случае сущ. решением ур-я Рикотти т.к. в этом случае ур-е явл. Ур-ем с разделенными переменными .
2) если q(x)=0 имеем лин. Ур-ние 3) если r(x)=0 то имеем ур-е Бернулли Если не выполяется ни одно из этих 3 условий , то ур-е Рикотти решить нельзя , неразрешимо в квыадратурах . Однако если эти три случая , но возможно найти хотя бы одно частное решение этого ур-я то ур-е решается в квадратуре . Установим это : пусть
тогда введем новую функцию z=z(x) Положем Подставив в уравнение получим
а это ур-е Бернулли |
Билет №23Уравнение в полных дифференциалах и их решение Пусть задано диф. ур-е ел. Вида:
где P(x,y) и Q(x,y) – непрер. Функции имеющие непрерыв часн. Производную 2 порядка включительно. Диф. ур. Назыв. Ур-ем в
полных диф-лах , если
т.е. ур. В этом случае имеет
вид : это уравнение явл полным диф. функции U как ф-ции двух переменных:
если выполняется равенство
тогда то левая часть
Теорема о необходимости и достаточности условия того что Ур было ур-ем в полных дифференциалах Теорема : Для того чтобы ур было ур-ем в полных диф. в некоторой Д принадл ХОУ Необх. И дост. Чтобы во всех точках обл. Д выполн
равенство
найдем |
Билет№21. Метод вариации производной постоянной при решении линейного диф. уравнения 1-го порядка. y’+P(x)y=Q(x) (1) -задано линейное неоднородное уравнение. Рассмотрим соотв. ему однородное уравнение y’=P(x)y=0 (2). Найдём общее решение:
Будем искать решение в том же виде, что и
однородного, только считая с не произвольной константой ,а функцией от
х :
|
Билет№19 Уравнения, приводящиеся к однородным.К таким уравнениям относят уравнения вида:
1) 2). 1). 2). Теперь допустим |
|
Билет №24 Интегральный множитель и его нахождение Пусть задано диф. ур-ние в диф. форме вида :
не всякое такое уравнение явл. Уравнением в полных
виференциалах однако доказано что для всякого такого ур-я может быть
подобрана ф-ция Найдем функцию определяющую интегр. Множитель данного уравнения:
тогда должно выполн. Рав-во:
имеем уравнение в частных производных относит неизв функции Мю.Общего метода нахожения которой не существует Найдем интегр множитель в случае если он явл ф-цией от одной из перемен. 1)Найдем условие при которых
2) Аналогично и
|
Вопрос №26. Уравнение вида: f(x,y¢)=0. 1) Предположим, что данное уравнение можно разрешить относительно y¢; y¢=fk(x), k=1,2,…
……………………………….
2) Пусть оно не разрешается относительно y¢ и разрешается относительно x. Пусть оно эквивал. Такому x=j(y¢). Будем искать решение данного уровнение в параметрической форме. y¢=p=p(x). Пусть x=j(p), А y ищем так: dx=j¢(p)dp dy=y¢dx=pj¢(p)dl. Отсюда Тогда общее решение 3) Предположим, что ур-ние
не разрешено не относ. х, не относ. y¢, но оно может быть представлено в виде с-мы двух
ур-ний, эквивалентных данному ур-нию: dy=y¢dx dx =j¢(x)dt dy=y(t)* j¢(t)dt Тогда парметрическое решение данное ур-я
|
Билет 28. Ур-ние Логранжа Ур. Лог.имеет следующий вид где ф-ция сменная производная по своему аргументу. Покажем что путём диф-ния и введения параметра можно получить общее решение в параметрической форме.Пусть у`=p=p(x) Подставляем в ур.
Продиф-ем на х
Рассмотрим два случая: 1)
Будем смотреть на это ур-ние как наур-ние от неизв. Ф-ции х, которая в свою очередь явл. Ф-цией параметра р.Тогда имеем обычное инт.ур.относительно неизв.ф-ции, которую можем найти. Пусть общим интегралом этого ур.будут F(p,е,c)=0 (2) Объеденим (2) и (1)
А это и есть общее решение ,представленое через параметр Р. 2) что удовлет. решению ур. : Пусть РI(I=1,2,..) будут решением этого ур. Тогда решением первоначального ур.А. будут ф-ции которые явл. Особыми решениями ур. А. И не могут быть получены общим решением. Ур.Клеро. Ур.Клеро имеет вид
аргументу. Вводим параметр Тогда Диф-ем по Х 1)
Если подставляем в (3)и получаем:
2)
Пример Замена
1)
общее решение:
|
|
Билет 27. Уравнение вида F(y,y`)=0 1)Пусть ур-ние разрешимо относ. y`,тогда y`=fk(y) Разрешим относ. y, где к=1,2….
Пустьfk(y) Считаем х-функцией от у.
Пусть fk(y)=0 . Тогда решен.данного ур-я могут быть ф-ции такие,которые удовлнтв.условиюF 2)Пусть ур-ние не разр.относ.у,, но разреш. отн. y, т.е. пусть наше
ур-е эквивал. Ур-нию
а)пусть
а тогда:
б) пусть у’=0, тогда у=const Решением ур-ния будут ф-ции у= какие удовлет.ур-ние F( Пример: решить ур. Разреш. относ. У .тогда
|
Билет 25. Рассмотрим несколько случаев: 1.Пусть задано следющее диф. ур-ние:
Это диф. ур-е 1-го порядка n-ой степени, где aI (x;y) – некото- рые непрырывные ф-ции двух переменных в некоторой обл. Q Ì R2 (i=0,…,n). Мы имеем ур-е n-ой степени относительно 1-ой производной, а известно, что всякое ур-е n-ой степени имеет вточности n-корней, среди которых есть как действительные так и комплексные. Пусть например это ур-е имеет какоето количество m £ n действительных корней. Т.к. коэффициенты этого ур-я являются ф-циями двух переменных, то ясно, что корни тоже будут ф-циями двух переменных. Пусть это будут решения y1=fk(x;y), k=1,2…m. Ур-е (1) свелось к m - ур-ий 1-го порядка. Пусть это ур-я, имеющие общий интеграл Fk=(x;y;c)=0, k=1,2…n. Тогда совокупность всех этих общих интегралов
и будет общим решением данного диф. ур-я (1). Пример:
Пусть x=0,а ур-ние разделим на x
Ур-я вида: F(y!)=0 Пусть заданное диф. ур-е явно зависит только от y! и не зависит явно от x и y. Тогда мы имеем некоторое алгебраическое ур-е относительно производных. А такое алгебраическое ур-е пусть имеет конечное или бесконечное множество действительных решений относительно производных. Т.е. y! = ki , i= 1,2… , где ki – некоторые действительные числа. У нас выполняется условие F(ki)º0. Решим ур-е y!=ki; y=kix+c; ki=(y-c)/x. Общий интеграл заданного диф. ур-я
Пример: (y!)4-4(y!)2+1=0 k4-4k2+1=0 действительные корни есть Значит сразу получаем общее решение
|


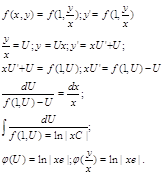
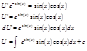
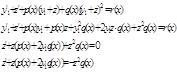
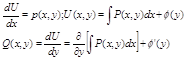
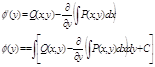
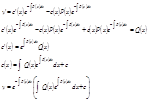
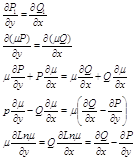
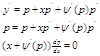
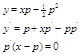
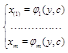 общее решен.х.
общее решен.х.