Быстрый поиск

Реферат: Полный курс лекций по математике

7. Сумма произведений элементов строки на алгебраические дополнения к элементам другой строки равна нулю.

Например, а11 А21+а12А22+а13А23=0.

Перечисленные свойства определителей справедливы для определителей любого порядка.

Пример. Вычислить определитель двумя способами.

первый способ. 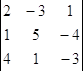= 2*5*(-3)+(-3)*(-4)*4+1*1*1 – (4*5*1+1*(-4)*2 + +(-3)*(-3)*1) = -30+48+1 – (20 – 8+9) = 19 – 21= -2.

Второй способ. Разложим определитель по элементам второго столбца. = -3 А12 + 5А22 + 1А32 = -3(-1)1+2 + 5(-1)2+2 +(-1)3+2 = -3*(-1)*(-3+16)+5(-6-4) – (-8 – 1) = 3*13+5*(-10) +9 = 48 – 50 = -2.

Системы линейных алгебраических уравнений. Решение систем по формулам Крамера.

Система линейных алгебраических уравнений имеет вид:

а11х1 + а12х2 + а13х3 = в1

а21х1 + а22х2 + а23х3 = в2

а31х1 + а32х2 + а33х3 = в3

Это система трех уравнений с тремя неизвестными х1, х2, х3. Вещественные числа аij (i = , j = ) называются коэффициентами системы. в1, в2, в3 – свободные члены. Если хотя бы одно из чисел в1, в2, в3, отлично от нуля, система называется неоднородной. Если все свободные члены равны нулю, то система имеет вид:

а11х1 + а12х2 + а13х3 = 0

а21х1 + а22х2 + а23х3 = 0

а31х1 + а32х2 + а33х3 = 0

и называется однородной.

По формуле Крамера решаются только неоднородные системы.

Определитель системы Δ называется определитель, составленный из коэффициентов системы:

Δ =

Если определитель системы Δ не равен 0, то система имеет единственное решение, которое находится по формулам:

Х1 = Δх1/ Δ; х2== Δх2/ Δ; х3== Δх3/ Δ; где

Δх1= ; Δх2= 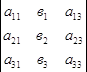; Δх3= .

Если определитель системы = Δ равен нулю, и хотя бы один из определителей ∆х1=∆х2=∆х3 отличен от нуля, то система несовместна.

Если определитель системы ∆=0, и ∆х1=∆х2=∆х3=0, то система имеет бесконечное множество решений. (неопределенная система).

Пример. Решить систему уравнений:

Х + 2у – z = 1

-3х + у = 2z = 0

х + 4у + 3z = 2

1) Вычислим определитель системы ∆ = = 1*1*3+2*2*1+(-1)*4*(-3) – (1*1*(-1)+4*2*1+3*2*(-3))=3+4+12 – (-1 + 8 – 18) = 19+11 = 30.

Система имеет единственное решение, т.к. определитель ∆ = 30 ≠ 0.

2) Вычислим определители ∆х, ∆у, ∆z.

∆х = 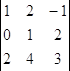= 5; ∆у = = 13; ∆z = = 1.

3) По формулам Крамера находим решение системы:

Х = ∆х/∆ = 5/30 = 1/6; у = ∆у/∆ = 13/30; z = ∆z/∆ = 1/30;

Ответ: решение системы (1/6; 13/30; 1/30).

По формулам Крамера можно решить систему n линейных уравнений с n неизвестными.

Пример Решить систему уравнений.

х - у+z=1

х + у – z=2

5х + у – z=7

1) Составим и вычислим определитель системы ∆= = 0.

2) Вычислим определители ∆х, ∆у, ∆z.

∆х =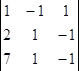 = 0, ∆у = 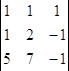= -2

Т.к. определитель ∆у= -2 ≠ 0, мы делаем заключение: Система несовместна, т.е. она не имеет решения.

Тема 7. Алгебра матриц.

Определение. Таблица, составленная из m*n чисел называется матрицей размерности m*n,

а11 а12 а13…а1п

а21 а22 а23…а2п

……………… = Ам*п= //аij//

ам1 ам2 ам3…амп , где

m – число строк, n – число столбцов. Числа аij называются элементами матрицы, i- номер строки, j – номер столбца, на пересечении которых стоит элемент.

Разновидности матриц.

1. Матрица называется прямоугольной, если m≠n.

2. Матрица называется квадратной, если m=n.

3. Матрица называется матрицей - строкой, если m=1.

4. Матрица называется матрицей - столбцом, если n=1.

Например, 1) 1 2 3 = А2*3 – прямоугольная матрица размерности 2*3 (два на три)

0 –1 5

2) 1 2 - квадратная матрица.

3 4

3) (1 0 3 5, -1) – матрица строка.

4) 7

12 матрица столбец.

5) Квадратная матрица называется треугольной, если все элементы матриц, расположенные выше или ниже главной диагонали равны нулю.

Например, 1 0 0 5 1 –3

2 6 0 или 0 4 2

-1 –2 8 0 0 -1

6) Квадратная матрица называется диагональной, если все ее элементы, кроме элементов главной диагонали, равны нулю.

Например, 1 0 0

0 –2 0

0 0 5

7) Квадратная матрица называется единичной, если элементы диагональной матрицы, стоящие на главной диагонали равны единице.

1 0 0

Е = 0 1 0

0 0 1 .

Алгебра матриц.

1. Равенство матриц. Две матрицы Ам*п и Вм*п одинаковой размерности равны, если равны соответствующие элементы этих матриц.

Ам*п = Вм*п ó аij = bij (i = , j = )

ó этот знак (квантор эквивалентности) заменяет слова «тогда и только тогда»,

обозначение (i = ) применяется, если хотят сказать, что i пробегает все значения от 1 до m.

2. Сумма матриц. Суммой двух матриц Ам*п = //аij// и Вм*п = //вij// называется матрица См*п, элементы которой Сij = аij + вij . Cm*n = Am*n + Bm*n. Складывать можно матрицы одинаковой соразмерности.

Нпример, Если А= 1 –2 4 В= -3 2 5

3 1 –6 , 1 –6 4 , то

=

=

+

А+В = 1 –2 4 -3 2 5 1-3 -2+2 4+5 -2 0 9

3 1 –6 1 –6 4 , 3+1 1-6 6+4 4 –5 –2

3. Умножение матрицы на число. Для того чтобы умножить матрицу на число надо каждый элемент матрицы умножить на это число.

3 2 4 –1

-2 1 5 6

αА = //α aij//.

12 8 16 –4

-8 4 20 24

3 2 4 –1

-2 1 5 6

Например, вычеслить 4 А, если А =

=

4А = 4 *

4. Умножение матриц. Произведением матрицы Ам*е на матрицу Ве*п называется матрица См*п (Ам*е*Ве*п=См*п), элементы которой получаются по правилу «Строка на столбец»:

сij =aijbij + ai2b2j +…+ aiebej

(i= ; j= ) , т.е. для вычисления сij следует элементы i – строки левой матрицы Ам*е умножить на соответствующие элементы j –го столбца правой матрицы Ве*п и полученные произведения сложить.

Замечание 1. Из этого определения следует, что произведение матриц имеет смысл тогда, когда число столбцов первого сомножителя равно числу строк второго сомножителя.

1 2

2 4

3 1

3 4 1 3

2 –1 –2 4

Замечание 2. Если имеют смысл АВ и ВА, то как правило, АВ≠ВА.

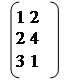
Пример. Вычислить АВ, если А = В =

Решение: АВ=С

С= * = =

С11=13+22=7;	С12=14+2(-1)=2	С13=11+2(-2)= -3	С14=13+24=11
С21=23+42=14;	С22=24+4(-1)=4	С23=21+4(-2)= -6	С24=23+44=22
С31=33+12=11	С32=3*4+1(-1)=11	С33=31+1(-2)=1	С34=33+14=13