Реферат: Синтез оптимальных уравнений

Для этого объекта рассмотрим задачу о быстрейшем попадании в начало координат (0, 0) из заданного начального состояния x0=(x01, x02). Иначе говоря, будем рассматривать задачу об оптимальном быстродействии в случае, когда конечным положением служит точка x1=(0, 0). Механически это означает, что материальную точку, имеющую заданное положение x01 и заданную начальную скорость x02, мы хотим за кратчайшее время привести в начало отсчёта с нулевой скоростью (т. е. добиться того, чтобы точка пришла в начало отсчёта и остановилась там).

Функция H в рассматриваемом случае имеет вид

H=ψ1x2+ψ2u                                                                                         (1.31)

(см. (1.29) и (B)). Далее, для вспомогательных переменных ψ1, ψ2 мы получаем систему уравнений . Из этой системы уравнений находим:       ψ1=d1;  ψ2= ─d1t+d2, где d1, d2 ─ постоянные интегрирования. Далее, в силу соотношения максимума (D) мы находим, учитывая (1.31) и (1.30):

u(t)= +1, если ψ2(t)>0;   u(t)= ─1, если ψ2(t)<0.

Иначе говоря, u(t)=sign ψ2(t)=sign (─ d1t + d2). Отсюда следует, что каждое оптимальное управление u(t), t0≤t≤t1, является кусочно-постоянной функцией, принимающей значения  и имеющей не более двух интервалов постоянства (ибо линейная функция ─d1t + d2 не более одного раза меняет знак на отрезке t0≤t≤t1).

Для отрезка времени, на котором u1, мы имеем (в силу системы (1.29)) 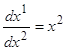, откуда находим

x1=1/2(x2)2+c.                                                                                       (1.32)

Таким образом, кусок фазовой траектории, для которого u1, представляет собой дугу параболы (1.32). Семейство парабол (1.32) показано на рис. 13 (они получаются друг из друга сдвигом в направлении оси x1). По этим параболам фазовые точки движутся снизу вверх (ибо = u1, т. е. ).

Аналогично для отрезка времени, на котором u ─1, мы имеем, откуда находим

x1= ─1/2(x2)2 + c’.                                                                                (1.33)

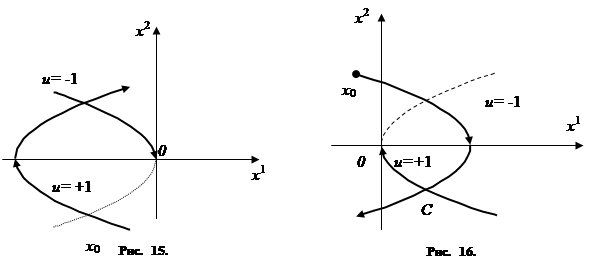
Семейство парабол (1.33) (также получающихся друг из друга сдвигом в направлении оси x1) показано на рис. 14. По параболам (1.33) фазовые точки движутся сверху вниз (ибо )

Как было указано выше, каждое оптимальное управление u(t) является кусочно-постоянной функцией, принимающей значения  и имеющей не более двух интервалов постоянства. Если управление u(t) сначала, в течение некоторого времени, равно +1, а затем равно ─1, то фазовая траектория состоит из двух кусков парабол (рис. 15), примыкающих друг к другу, причём второй из этих кусков лежит на той из парабол (1.33), которая проходит через начало координат (ибо искомая траектория должна вести в начало координат). Если же, наоборот, сначала u= ─1, а затем u= +1, то мы получаем фазовую траекторию, изображённую на рис. 16. На рис. 15, 16 надписаны на дугах парабол соответствующие значения управляющего параметра u.

На рис. 17 изображено всё семейство полученных таким образом фазовых траекторий (здесь AO ─ дуга параболы x1=1/2(x2)2, расположенная в нижней полуплоскости; BO ─ дуга параболы x1= ─1/2(x2)2, расположенная в верхней полуплоскости).

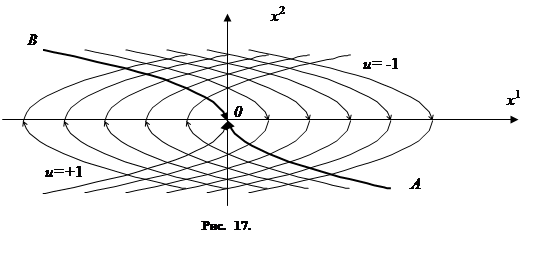Итак, согласно принципу максимума только изображённые на рис. 17 траектории могут быть оптимальными, причём видно, что из каждой точки фазовой плоскости исходит только одна траектория, ведущая в начало координат, которая может быть оптимальной (т. е. задание начальной точки x0 однозначно определяет соответствующую траекторию).

8.   Проблема синтеза оптимальных управлений. Посмотрим на разобранный в предыдущих пунктах пример с несколько иной точки зрения. Найденное выше решение оптимальной задачи можно истолковать следующим образом. Обозначим через v(x)= +1 ниже линии AOB и на дуге AO, v(x)= ─1 выше линии AOB и на дуге BO. Тогда (см. 17) на каждой оптимальной траектории значение u(t) управляющего параметра (в произвольный момент времени t) равно v(x(t)), т. е. равно значению функции v в той точке, в которой в момент t находится движущаяся фазовая точка, пробегающая оптимальную траекторию u(t)=v(x(t)). Это означает, что, заменив в системе (1.29) величину u функцией v(x), мы получим систему

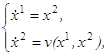                                                                                  (1.34)

решение которой (при произвольном начальном состоянии x0) даёт оптимальную фазовую траекторию, ведущую в начало координат. Иначе говоря, система (1.34) представляет собой систему дифференциальных уравнений (с разрывной правой частью) для нахождения оптимальных траекторий, ведущих в начало координат.

Рассмотренный пример показывает, что решение задачи об оптимальных управлениях естественно ожидать в следующей форме. Будем решать оптимальную задачу в общей постановке:

 

(см. п. 3), рассматривая всевозможные начальные состояния и каждый раз предписывая в качестве конечного состояния начало координат O фазового пространства. Тогда (насколько можно судить по разобранному выше примеру) существует такая функция v(x), заданная в фазовом пространстве V принимающая значения в области управления U, что уравнение

                                                                                  (1.35)

определяет все оптимальные траектории, ведущие в начало координат. Иначе говоря, оптимальное управление оказывается естественным искать не в форме u=u(t), а в форме u=v(x), т. е. искомое оптимальное управление в каждый момент зависит лишь от того, в какой точке пространства находится в данный момент фазовая точка.

Функцию v(x), дающую уравнение оптимальных траекторий в форме (1.35), называют синтезирующей функцией, а задачу нахождения синтезирующей функции ─ задачей синтеза оптимальных управлений. В разобранном примере синтезирующая функция была кусочно-непрерывной (даже кусочно-постоянной).

Г л а в а II

ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ

§ 4.  Линейная задача оптимального управления

9.   Формулировка задачи. Ниже будут подробно изучены управляемые объекты, движение которых описывается линейными дифференциальными уравнениями относительно величин x1,…,xn, u1,…,ur, т. е. уравнениями вида

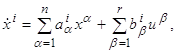 i=1,2,…,n,                                                (2.1)

где aiα и biβ ─ некоторые постоянные коэффициенты.

Одним из наиболее важных для приложений является случай, когда каждая из величин u1,u2,…,ur в уравнениях (2.1) представляет собой отдельный управляющий параметр, область изменения которого не зависит от значений остальных управляющих параметров и задаётся неравенствами

 β=1,…,r.                                                                     (2.2)

Как было указано выше (см. п. 4), эти неравенства определяют r-мерный параллелепипед.

В дальнейшем при рассмотрении объектов вида (2.1) будет предполагаться, что управляющий параметр u=(u1, u2,…, ur) может меняться в замкнутой области управления U, представляющей собой выпуклый многогранник (лежащий в пространстве переменных u1, u2,…, ur).

Для того чтобы записать уравнения (2.1) в векторной форме, мы введём в рассмотрение матрицы

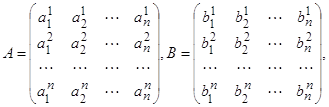                             (2.3)

элементами которых являются коэффициенты aiα, biβ, входящие в уравнения (2.1). Как обычно, результат применения матрицы A к вектору x=(x1, x2,…, xn) мы будем обозначать символом Ax, т. е. y=Ax есть n-мерный вектор, координаты которого определяются формулами

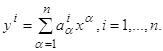                                                                      (2.4)

Аналогично для любого r-мерного вектора u=(u1, u2,…, ur) через Bu обозначается вектор, i-я координата которого равна 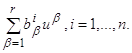 Таким образом, матрица A определяет линейное отображение координатного n-мерного пространства снова в n-мерное пространство, а матрица B определяет отображение r-мерного пространства в n-мерное.

Пользуясь матрицами A и B, мы можем теперь записать уравнения (2.1) в векторной форме:

                                                                                          (2.5)

Пусть u(t)=(u1, u2,…, ur) ─ произвольное допустимое (в смысле п. 4) управление, заданное на некотором отрезке t0≤t≤t1, и x0=(x10,…, xn0) ─ некоторая точка фазового пространства. Обозначим θ1, θ2,…, θk все точки, в которых хотя бы одна из функций  u1(t), u2(t),…, ur(t) терпит разрыв, причём занумеруем эти точки таким образом, что t0<θ1<θ2<…<θk<t1. Подставив функции u1(t), u2(t),…, ur(t) в правые части системы (2.1),мы придём к системе уравнений

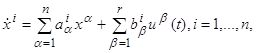                                               (2.6)

или в векторной форме,

                                                                                      (2.7)

Систему (2.7) мы рассмотрим сначала для значений t, удовлетворяющих неравенствам t0≤t≤θ1. На этом отрезке изменения аргумента существуют такие функции x1(t),…, xn(t), определённые и непрерывные на всём отрезке t0≤t≤θ1, которые, рассматриваемые на интервале t0<t<θ1, являются решениями системы (2.6) и, кроме того, удовлетворяют начальным условиям x1(t0)=x10, x2(t0)=x20,…, xn(t0)=xn0 (согласно сведениям из дифференциальных уравнений (см. книгу Л.С. Понтрягина «Обыкновенные дифференциальные уравнения», «Наука», М., 1965 (стр. 23, 24 и 168-172))).

Теперь мы можем рассмотреть систему (2.6) на отрезке θ1≤t≤θ2, воспользовавшись точкой γ1=(x1(θ1),…, xn(θ1), θ1) в качестве начального значения. На отрезке θ1≤t≤θ2 снова существует решение с начальным значением γ1. Это решение мы снова обозначим через x(t)=(x1(t),…, xn(t)). Теперь функция x(t) построена на отрезке t0≤t≤θ2 и непрерывна на всём этом отрезке (и, в частности, в «точке сопряжения» θ1;). Воспользовавшись, далее, новым начальным значением γ2=(x1(θ2),…, xn(θ2), θ2), мы продолжим эту функцию x(t) на отрезок θ2≤t≤θ3 и т. д. В конце концов мы определим x(t) на всём отрезке t0≤t≤t1.

Полученная функция x(t)=(x1(t),…, xn(t)) непрерывна на всём отрезке t0≤t≤t1 и является на нём кусочно-дифференцируемой; именно, во всех точках интервала t0<t<t1, кроме θ1, θ2,…, θk, функция x(t) непрерывно дифференцируема (и удовлетворяет системе (2.6)). Построенную функцию мы будем называть решением системы (2.6) (или уравнения (2.7)), соответствующим управлению u(t), при начальном условии x1(t0)=x10, x2(t0)=x20,…, xn(t0)=xn0. Наконец, мы будем говорить, что допустимое управление u(t), t0≤t≤t1, переводит фазовую точку из состояния x0 в состояние x1 (в силу закона движения (2.1) или (2.5)), если соответствующее ему решение x(t) системы (2.1), удовлетворяющее начальному условию x(t0)=x0, приходит в момент t1 в точку x1, т. е. удовлетворяет также «конечному» условию x(t1)=x1.

Теперь можно уточнить постановку задачи.

Линейной задачей оптимального управления мы будем называть задачу об отыскании оптимальных быстродействий в случае, когда выполнены следующие три условия:

1 )   уравнения движения объекта линейны (см. (2.1) или (2.5));

2 )   предписанное конечное состояние x1 совпадает с началом координат (0, 0,…, 0) n-мерного фазового пространства переменных x1, x2,…,xn;

3 )   область управления U является r-мерным выпуклым многогранником в r-мерном пространстве (u1, u2,…, ur), причём начало координат этого пространства принадлежит многограннику U, но не является его вершиной.

Заметим, что начало координат xi=0, i=1,…,n, является положением равновесия системы

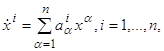                                                                      (2.8)

получающейся из системы (2.1) отбрасыванием управлений (т. е. получающейся из (2.1) при u1=u2=…=ur=0). Таким образом, условие 2) означает, что ищется управление, переводящее объект из заданного начального состояния x0 в положение равновесия.

Страницы: 1, 2, 3, 4, 5