Реферат: Синтез оптимальных уравнений
10. Принцип максимума. В пункте 6 мы сформулировали необходимое условие оптимальности, называемое принципом максимума. Данный пункт посвящён принципу максимума в случае линейной задачи оптимального управления. Вначале укажем те упрощения в формулировке принципа максимума, которые возникают в этом частном случае (т. е. в случае линейной задачи оптимального управления).
Заметим, прежде всего, что функция H (см. формулу (B) на стр. 10) принимает вид
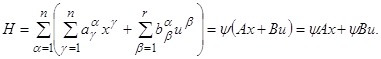(2.9)
(Здесь в правой части записаны скалярные произведения; например, ψAx есть скалярное произведение векторов ψ и Ax.)
Далее, рассмотрим систему дифференциальных уравнений для вспомогательных переменных ψ1, ψ2,…, ψn (см. формулу (C) на стр. 10). Мы имеем
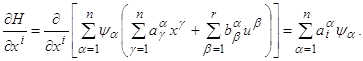
Следовательно, система уравнений для вспомогательных переменных принимает вид
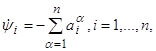(2.10)
т. е. представляет собой так называемую сопряжённую систему (по отношению к линейной системе (2.8)). В векторной форме система (2.10) записывается в виде
(2.11)
где
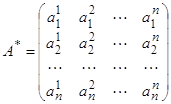
─ матрица, получающаяся из матрицы A транспонированием (т. е. заменой строк столбцами).
Так как в правой части соотношения (2.9) первое слагаемое совсем не зависит от u, то при написании соотношения (D) (см. стр. 11) достаточно рассмотреть лишь второе слагаемое. Таким образом, соотношение (D) принимает в рассматриваемом случае вид
(2.12)
для любого момента τ, t0≤τ≤t1.
Наконец, соотношение (E) (стр. 11) становится просто ненужным, так как в рассматриваемом случае оно всегда выполняется. Действительно, так как x(t1)=(0, 0,…, 0) (условие 2) на стр. 15), то в H(ψ(t1), x(t1), u(t1)) первое слагаемое обращается в нуль (см. (2.9)). Второе же слагаемое, в силу (2.12), заведомо неотрицательно, ибо при u1=…=ur=0 (эта точка, в силу условия 3) на стр.15, принадлежит многограннику U) мы имеем ψ(τ)Bu=0, а потому максимальное значение выражения ψ(τ)Bu неотрицатнльно. Итак, соотношение H(ψ(t1), x(t1), u(t1))³0 для линейной оптимальной задачи всегда выполнено.
Сказанное можно резюмировать следующим образом. Пусть u(t), t0£t£t1, - допустимое управление, переводящее объект (2.5) из заданного начального состояния x0 в положение равновесия (0, 0,…, 0). Будем говорить, что управление u(t) удовлетворяет принципу максимума, если существует такое нетривиальное решение y(t) уравнения (2.11), для которого выполняется условие максимума (2.12) (в каждый момент времени t, t0£t£t1). Для оптимальности управления u(t) необходимо, чтобы оно удовлетворяло принципу максимума. Это и есть та упрощённая формулировка принципа максимума, к которой мы приходим в случае линейной задачи оптимального управления.
11. Принцип максимума — необходимое и достаточное условие оптимальности. Замечательным фактом является то, что в случае линейной задачи оптимального управления принцип максимума представляет собой не только необходимое, но и достаточное условие оптимальности. Однако факт этот имеет место не для произвольной линейной задачи — имеются малосущественные исключения. Поэтому мы наложим на линейную задачу некоторое ограничение, называемое условием общности положения. Сформулируем это условие:
Условие общности положения: если w — вектор, параллельный произвольному ребру многогранника U, то вектор Bw не принадлежит никакому собственному инвариантному подпространству относительно преобразования A. Невыполнение условия общности положения означает, что хотя бы для одного ребра многогранника U векторы Bw, ABw, A2Bw,…, An-1Bw линейно зависимы, т. е. определитель n-го порядка, составленный из координат этих векторов, обращается в нуль. Однако всюду в дальнейшем условие общности положения предполагается (если не оговорено противное) выполненным.
Теперь перейдём к теореме, упоминавшейся в начале этого пункта.
Т е о р е м а 2.1. Пусть u(t), t0£t£t1, — допустимое управление, переводящее объект из заданного начального состояния x0 в положение равновесия (0, 0,…, 0). Для оптимальности управления u(t) необходимо и достаточно, чтобы оно удовлетворяло принципу максимума.
12. Основные теоремы о линейных оптимальных быстродействиях.
Т е о р е м а 2.2. Для каждого нетривиального решения y(t) уравнения (2.11) соотношение (2.12) однозначно определяет допустимое управление u(t); при этом оказывается, что функция u(t) кусочно-постоянна и её значениями являются лишь вершины многогранника U.
Каждую точку разрыва оптимального управления мы будем называть точкой переключения.
Т е о р е м а 2.3. Предположим, что многогранник U является r-мерным параллелепипедом (2.2) и что все собственные значения матрицы A=(aij), составленной из коэффициентов уравнений (2.1), действительны. Тогда в оптимальном управлении u(t)=(u1(t),…, ur(t)) каждая из функций ub(t), b=1,…,r, кусочно-постоянна, принимает только значения ab и bb (см. (2.2)) и имеет не более n-1 переключений (т. е. не более n интервалов постоянства), где n — порядок системы (2.1).
Т е о р е м а 2.4 (т е о р е м а е д и н с т в е н н о с т и). Пусть u1(t) и u2(t) — два оптимальных управления, заданных соответственно на отрезках t0£t£t1 и t0£t£t2 и переводящих точку x0 в начало координат. Тогда эти управления совпадают, т. е. t1=t2 и u1(t)ºu2(t) на отрезке t0£t£t1.
Областью управляемости для объекта (2.5) мы будем называть множество всех точек x0 фазового пространства X, из которых возможно при помощи какого-либо допустимого управления попасть в начало координат. Само начало координат мы также будем причислять к области управляемости. Ясно, что вопрос о нахождении оптимальных процессов разумно ставить лишь в случае, если начальное фазовое состояние x0 принадлежит области управляемости (ведь из точек, не принадлежащих области управляемости, вообще нельзя попасть в начало координат).
Т е о р е м а 2.5 (т е о р е м а с у щ е с т в о в а н и я). Область управляемости является выпуклым открытым множеством фазового пространства X; для любой точки x0, принадлежащей области управляемости, существует оптимальное управление, переводящее точку x0 в начало координат.
Т е о р е м а 2.6. Если в линейной задаче оптимального управления матрица A (см. (2.3)) устойчива, т. е. все её собственные значения имеют отрицательные действительные части, то область управляемости совпадает со всем фазовым пространством X. Следовательно, для любой точки x0ÎX существует оптимальное управление, переводящее фазовую точку x0 в начало координат.
§ 5. Решение задачи синтеза для линейных задач второго порядка
13. Упрощение уравнений линейного управляемого объекта. Нередко бывает, что в линейной задаче общая запись уравнений движения объекта в виде (2.1) неудобна и целесообразно воспользоваться некоторыми упрощениями. Мы здесь отметим стандартные упрощения, которые можно осуществить с помощью замены координат.
q Прежде всего, рассмотрим вопрос о замене координат в фазовом пространстве X рассматриваемого управляемого объекта. Предположим, что в пространстве X вместо координат x1,…, xn введены новые координаты y1,…, yn, связанные с прежними координатами соотношениями
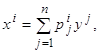
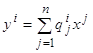(2.13)
(где матрицы P=(pij) и Q=(qij) взаимно обратны). Ясно, что при такой замене линейная система (2.1) превращается в новую линейную систему
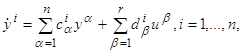
коэффициенты которой легко вычисляются:
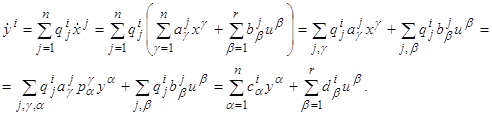
Таким образом,
, 
Переходя к
векторным обозначениям, можно сказать, что указанная замена координат переводит
уравнение (2.5) в уравнение 
где
матрицы C и D
выражаются через матрицы A, B,
P, Q по
формулам C=QAP,
D=QB.
Очевидно, при
такой замене условия 1), 2), указанные на стр. 15, сохраняются и для уравнения
получаемого после замены.
Далее, каждый процесс (u(t),
x(t)), удовлетворяющий
уравнению 
переходит в процесс (u(t), y(t)), удовлетворяющий уравнению 
(и обратно). Так как при
этом время t не меняется, то указанная замена переводит
оптимальные процессы для уравнения 
(и
наоборот). В частности, синтез оптимальных управлений для уравнения 
переводится с помощью
преобразования координат (2.13) в синтез оптимальных управлений для уравнения 
.
Таким образом, если уравнение 
окажется
проще и для него синтез оптимальных управлений можно будет построить, то из
этого синтеза можно (с помощью афинного преобразования (2.13)) получит синтез и
для первоначального уравнения 
. В этом
и заключается смысл замены координат (2.13): она позволяет заменить матрицу A трансформированной матрицей C=QAP, в то же время вызывая лишь афинное искажение картины
синтеза оптимальных управлений. Таким образом, преобразованием (2.13) можно
воспользоваться для упрощения матрицы A,
составленной из коэффициентов при фазовых координатах.
q Предположим,
что в уравнении 
матрица A уже приведена к простейшему виду (с помощью описанного
выше приёма). Укажем теперь, каким образом может быть упрощена матрица B, составленная из коэффициентов при управляющих
параметрах.
С этой целью положим
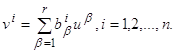(2.14)
Это означает, что вместо r управляющих параметров u1,…,ur вводятся n других управляющих параметров v1,…, vn, благодаря чему система (2.1) заменяется следующей:
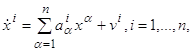
или в
векторной форме, 
Нужно только выяснить, в каких пределах может изменяться точка v=(v1, v2,…, vn). Удобно считать, что эта точка v=(v1, v2,…, vn) расположена в том же пространстве X, что и точка x=(x1,…, xn).
Соотношения (2.14) определяют линейное отображение r-мерного пространства переменных u1,…,ur в фазовое пространство X. Образом многогранника U при отображении (2.14) является некоторый выпуклый многогранник в пространстве X, который мы обозначим через V.
Таким образом, получаем два линейных уравнения:
(2.15)
(2.16)
Г л а в а III
СИНТЕЗ ОПТИМАЛЬНЫХ УПРАВЛЕНИЙ ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
§ 6. Решение задачи синтеза в случае комплексных собственных значений
14. Задача синтеза для малых колебаний маятника. Здесь будет дано полное решение задачи синтеза оптимальных управлений для линейных объектов, описываемых уравнениями второго порядка. Фазовое пространство X в этом случае представляет собой плоскость.
Рассмотрим колебание плоского маятника. Как известно колебание маятника, подвешенного к точке опоры, описывается дифференциальным уравнением второго порядка:
(в нашем случае положим β=1)
при малых колебаниях маятника Sinφ≈φ тогда уравнение движения маятника запишется в виде:
(3.1)
Управляющий параметр u (скалярный) будем предполагать изменяющимся в пределах -1£u£1.
Пусть 
— угол отклонения, а 
— скорость маятника. Тогда
уравнение (3.1) перепишется в виде следующей нормальной системы:
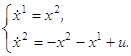(3.2)
На плоскости x1, x2 «многогранник» U будет представляться отрезком [-1, 1], расположенным на оси x2. Легко видеть, что ось x2 не является собственным инвариантным подпространством матрицы A, которая для системы (3.2) имеет вид:
A=
,
и потому условие общности положения всегда выполнено.
Найдём собственные значения матрицы A. Для этого составим характеристическое уравнение |λE─A|=0, т. е. λ2+λ+1=0. Откуда находим, что собственные значения матрицы A такие:
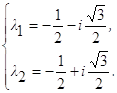
т. е. собственные значения
матрицы A комплексные. Введём обозначения 
где b≠0.
Тогда матрица A преобразуется к виду:
=
.
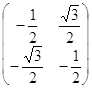Будем
рассматривать систему, соответствующую матрице 
,
т. е. систему вида:
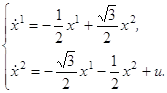(3.3)
Вначале рассмотрим соответствующую однородную систему:
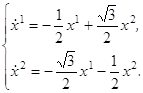(3.4)
Общее решение этой системы имеет вид:
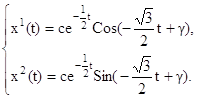
где c, γ – произвольные постоянные интегрирования.
Запишем функцию H и применим принцип максимума.
где ψ1, ψ2 определяются системой, сопряжённой к системе (3.3), т. е. системой вида:
(3.5)
Общее решение этой системы имеет вид:
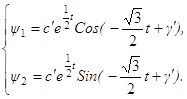
где c’, γ’ – произвольные постоянные интегрирования. Т. е. функция H имеет вид:
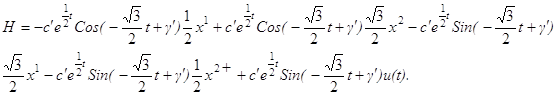
Подставим в функцию H представление решений x1, x2:
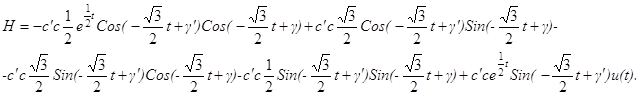
Т. к. собственный вектор матрицы A, соответствующий собственному значению l имеет вид q1─iq2, где q1=(1;─1/2);
q2=(0;─
).
Пусть q1 и q2 – базисные векторы новой косоугольной системы координат y1, y2. Тогда переход от системы y1, y2 к системе x1, x2 выражается формулами:
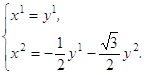
Тогда в новых координатах система уравнений (3.2) запишется в виде
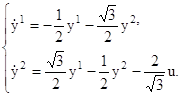
или, иначе, в виде
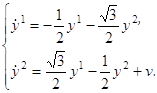
где v=(v1, v2)
─ управляющая точка, которая может меняться в пределах многогранника V, представляющего собой отрезок [
] оси y2.
Согласно
теории вершинам e1=(0, 
), e2=(0,
) многогранника V соответствуют точки h1=(1,
-
),
h2=(-1, 
)
(координаты указаны в системе y1, y2), а каждый из углов a1, a2, соответствующих
этим вершинам, равен p.
Теперь уже нетрудно построить синтез оптимальных управлений в плоскости y1, y2. Кусками фазовых траекторий будут дуги логарифмических спиралей, т. к. у нас b=1, т. е. b>0 (рис. 18).
При переходе от координат y1, y2 к координатам x1, x2 картина синтеза афинно искажается.
